26 sandías en el camino a Almería

—¡Toma! Yo quiero ésta, es gordísima…

—Pero, ¡Ven! —dijo su primo Jose —¡Ésa casi no cabe en el maletero!

—Ven no se cansa nunca de comer sandía —añadió Sal divertido.

—Es que la playa me abre el apetito —respondió Ven —Me lo ha dicho mamá.

Volvían de pasar el día en la playa de Mónsul con Mati y Gauss. Ella había parado el coche para comprar una sandía a un señor que las vendía en la carretera.

—Es increíble que no se caigan rodando, ¿verdad? —preguntó Jose a sus primos.

—Supongo que como no son esferas perfectas… —empezó a decir Sal —no podrán rodar, ¿no?

—¿Qué? ¿Ya habéis elegido la sandía que nos llevaremos? —se acercó Mati a preguntarles —¿O le preguntamos mejor al señor que sabrá cuál es más jugosa?

—¿Por qué no se caen, Mati? —le preguntó Jose —¿Porque no son esferas perfectas?

—No, si lo fueran, tampoco se caerían —respondió la pelirroja —Además este señor las tiene apiladas de la mejor forma posible, como le gustaría a Kepler.

—¿Kepler es el frutero de tu barrio, Mati? —preguntó el pequeño Ven.

—No, no, cielo —dijo ella sonriendo —Johannes Kepler era una famoso astrónomo y matemático alemán, según mucha gente, una de las piezas fundamentales en la revolución científica del siglo XVII.

—¿Y le gustaban mucho las sandías? —insistía Ven.

—Pues no lo sé —respondió Mati —Pero sí que le gustaba mucho mirar al cielo como a vosotros y a Mister Green. De hecho, fue él el que enunció las leyes que describían el movimiento de los planetas alrededor del Sol y hasta se atrevió a ¡diseñar un telescopio!

—Qué tío… —mascullaba Jose.

—¿Y qué tiene que ver todo esto con las sandías, Mati? —seguía insistiendo Ven.

—¿Kepler era amigo de Galileo, Mati? —preguntó Sal.

—Bueeeeeno… —respondió ésta —amigos, amigos, no diría yo. Parece que a Galileo no llegaron a gustarle mucho los trabajos de Kepler, creo que le molaban más los de Copérnico...

—¿Que qué tiene que ver un telescopio con una sandía? —el pobre Ven se estaba desesperando.

—Huy, es cierto, cielo —dijo Mati acariciando el pelo del pequeño con dulzura —Pues para entender qué tiene que ver Kepler con las sandías, os contaré una historia de caballeros y batallas navales.

Los tres niños se sentaron junto a la montaña de sandías, Gauss se acurrucó junto a Jose. El frutero les dio un trozo de sandía a cada uno que comían con ganas porque venían acalorados.

—Hace mucho tiempo —comenzó a contarles Mati —en el siglo XVI, un barco inglés que se llamaba El Tigre navegaba camino de América. El jefe de la expedición era un caballero inglés Sir Walter Raleigh.

—Seguro que era muy valiente… —interrumpió Jose.

—Sí, eso dicen —corroboró Mati —Muy valiente y ¡muy guapo! Dicen que la reina Isabel I se fijó en él cuando a l ir a cruzar ella por un sitio donde había mucho barro, Wlalter Raleigh, todavía no era Sir, se quitó la capa que llevaba y la puso en el suelo para que la reina no se manchara los pies.

—Qué guarro… —dijo de nuevo Jose.

—Bueno, parece que a la reina le gustó el gesto y lo nombró caballero —terminó de decir Mati.

—Jo, qué suertudo… —insistía el primo de Sal y Ven.

—Lo cierto, Jose, es que esto último no está tan claro, hay quien dice que fue leyenda aumentada por los rumores —continuó Mati —Otras fuentes apuntan a que la reina lo nombró caballero por unos trabajitos que Raleigh hizo en Irlanda para que no se rebelaran contra la reina…

—Vamos, Mati, a las sandías… —Ven estaba poniéndose nervioso.

—A las sandías —dijo ella —En el mismo barco, viajaba Thomas Harriot, un matemático que trabajaba para Sir Walter Raleigh, también astrónomo. Pues bien, dicen que Raleigh le preguntó a Harriot por qué siempre apilaban las balas así…

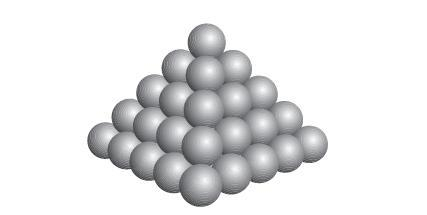
— .También le propuso a Harriot que calculara cuántas balas podía tener la pirámide, en función de su base…

—¿Cuántas? —preguntó Sal.

—¿Lo intentamos calcular? —propuso Mati.

—¡Vale! —dijo Jose.

—Y seguimos sin hablar de las sandías… —masculló Ven.

—Bueno, Ven —dijo la pelirroja —Puedes pensar en sandías en lugar de balas de cañón, ¿quieres?

—No, venga…con balas de cañón… —dijo el pequeño.

—Vamos a calcular entre todos cuántas balas habrá en una pirámide base cuadrada, de lado 4 —propuso Mati —en la primera capa habrá…

—¡16 sandías! —se apresuró a decir Jose.

—Ponemos la segunda capa… —decía Mati.

—¡9 sandías! —gritó Ven.

—¡En la tercera 4, Mati! —dio Jose.

—Y por último, 1 en la última capa —concluyó Mati —Ya podemos sumar

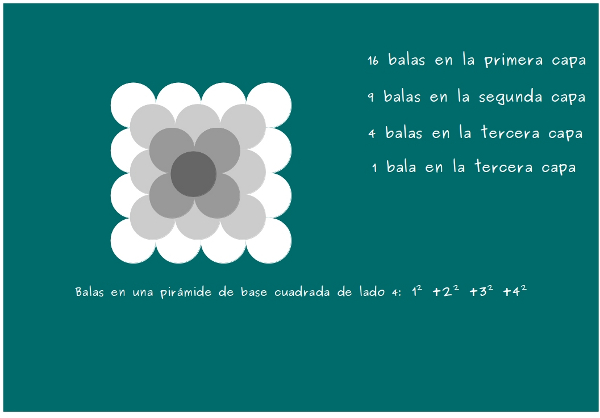
—Y fijaos qué curioso —les advirtió a los niños —Podemos obtener una fórmula para calcular el número de balas…

—O de sandías.. —apuntó Ven.

—Eso, o de sandías, que hay en cualquier pirámide de base cuadrada.

—Así que si tenemos una pirámide con una base cuadrada de lado 6, tendrá…

—¡Toma, toma, toma! ¡Cómo mola! —dijo Jose.

—No me imites, Jose… —protestó con una sonrisilla Ven al que en el fondo le había gustado que su primo lo imitara.

—¿Lo hacemos con las pirámides de bases triangulares? —preguntó Mati

—¡Sí! —contestaron los tres niños a la vez.

—Vamos a contar las balas que tienen las pirámides más pequeñitas —empezó a decir la gafotas —a ver si deducimos una fórmula que me permita calcular el número de balas en cualquier pirámide de base triangular, como las estamos construyendo, poniendo cada esfera en el hueco que queda entre las cuatro que están justamente debajo.

Los niños empezaron a pintar en la pizarra de Mati las pirámides de base triangular de lados 2, 3 y 4, y a contar las balas que las componían.

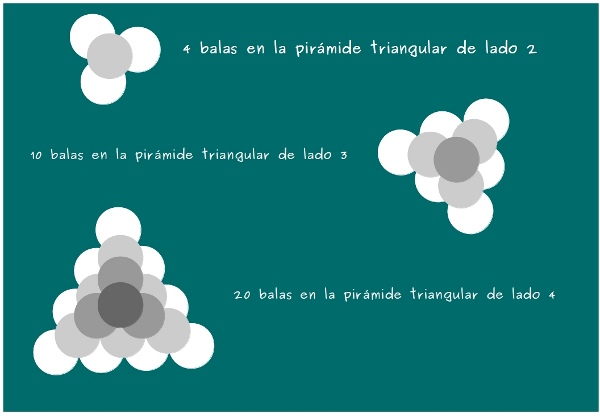
—Muy bien, chicos —les animó —Ahora la de lado 5.

—Ahora vamos a fijarnos en los números que hemos ido obteniendo para ver si podemos deducir una fórmula que nos sirva para calcular cuántas balas o sandías hay en un pirámide de base triangular, conociendo sólo cuántas balas hay en el lado del triángulo de la base —les propuso Mati —Llamaremos PT₂ al número de balas en la pirámide triangular de lado 2 en la base, PT₃ al correspondiente en la de base 3 y, en general, PT_N al que indica el número de balas en la pirámide de base triangular con N balas en el lado de la base. Fijaos lo que sale…

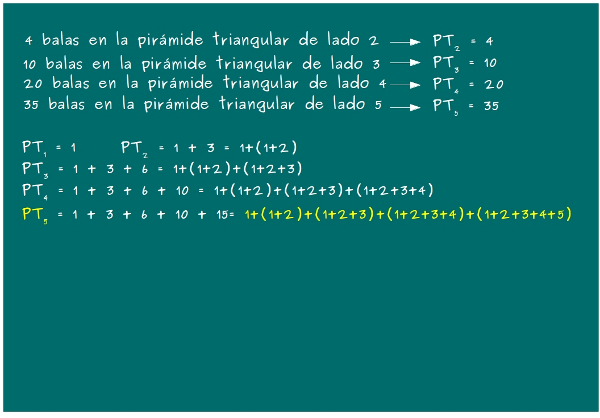
—¿Y ahora qué, Mati? —preguntó Jose ansioso.

—Pues que podemos ver una fórmula para PT_N —dio ésta —Puesto que cada pirámide es igual a la anterior, más una base de lado N que tiene (1+2+3+…+N) balas.

—Pero vosotros ya sabéis cuál es la fórmula para calcular (1+2+3+…+N), ¿verdad? —les preguntó Mati.

—¡Sí! —gritó el gafotas —Y la descubrió Gauss. Es N por N+1 partido por 2.

Gauss ladró orgulloso, le encantaba oír su nombre cuando se trataban temas tan importantes…

—Pues con ésa fórmula y con la que hemos visto antes para la suma de los cuadrados, de puede deducir lo siguiente:

—Así —continuó la gafotas —Si queremos calcular cuántas balas habrá en una pirámide de base triangular de lado 12 balas en la base…

—¡Toma, toma, toma! ¡Cómo mola! —dijeron al unísono Jose y Ven.

—Pues sí, mola mucho —continuó Mati —Tanto que Harriot se quedó pensando sobre el tema y como además le gustaba estudiar sobre átomos y tal, se hizo preguntas bastante más complicadas como, por ejemplo, ¿cuál es la forma óptima de apilar esferas para aprovechar al máximo el espacio?

—¿Cuál es? —preguntó ansioso Sal.

—Ahora es cuando entra nuestro amigo Kepler en escena —Mati guiñó un ojo —Porque Harriot le escribió a Kepler hablando sobre estos problemas y claro, Kepler que era muy curioso, se puso a trabajar sobre el asunto y…

—¿¿Y?? —preguntó Sal con impaciencia.

—Pues que Kepler conjeturó que la mejor forma de empaquetar esferas era precisamente, así, como apilan las frutas los fruteros —dijo Mati —Poniendo las esferas en cada capa de forma que éstas se apoyen en el hueco que forman las cuatros esferas que están debajo de ellas.

—¿Y era verdad, Mati? —preguntó de nuevo el gafotas.

—Pues sí, era verdad —respondió ella —Pero no se ha demostrado hasta 2005.

—Yo ya había nacido, Mati —gritó Ven —Pobre Kepler, nunca supo que se había demostrado…

—¿Quién lo demostró, Mati? —preguntó Jose.

—Pues otro Thomas, Thomas Hales, un matemático norteamericano —contestó Mati.

—Qué crack… —apuntó jose

—¿Está muerto? —preguntó Ven con carita de pena.

—No, es un hombre joven aún, Ven, no te preocupes —lo tranquilizó ella.

—¿Y por qué tardaron tantos años en demostrar esto? —preguntó Sal muy serio.

—En matemáticas, a veces, las preguntas aparentemente más simples pueden tener una solución muy complicada —concluyó la gafotas.

—O sea que los fruteros son expertos en matemáticas, ¿no, Mati? —preguntó Ven con la cara absolutamente manchada de sandía.

—Eso es, Ven —dijo ella con una sonrisa —Aunque el que parece que se entiende bien con las esperas es nuestro Gauss…

FIN

Pues sí, la historia sobre la conjetura de Kepler tiene todos los ingredientes necesarios para ser una gran aventura. Hace poco tiempo, estaba tomando café con mi amigo Daniel y me sugirió que se la contase a mis chicos. Así que pensé, ¡qué buena idea, Dani!

Ésta es una versión resumida y sin entrar mucho en los detalles más técnicos del camino recorrido desde Kepler hasta la demostración de Hales, pero si os interesa entrar en detalle, os recomiendo esta entrada de mi amigo Daniel en su blog “La aventura de la ciencia“.

La demostración de Hales requiere el uso de computadores para unos cálculos muy complicados y suscitó alguna polémica entre matemáticos por ello. Alguno incluso se atrevió a criticarla sin informarse demasiado como nos explica Francisco Santos en esta carta al director de El País.

Volveremos otro día a jugar con esferas, hasta entonces, ¡Feliz fin de semana!

MATI