En principio 44 palomas

—No lo entiendo, Sal, ¿qué quieres que te diga?

—A ver, Ven –dijo el gafotas muy tranquilo –, como son 10 palomas y solo hay 3 palomares, no puedes poner 4 palomas en cada uno…

—Toma, claro –interrumpió el pequeño –, eso es imposible, Sal.

—Entonces –continuó su hermano –, en un palomar tiene que haber menos de 4…

—O en 2 palomares –volvió a interrumpir su hermano –. Puede haber 8 en uno, y en los otros 2 solo una paloma en cada uno.

—Sí, sí, ya… —aceptó Sal y se quedó pensativo.

—¿Qué? ¿Leyendo nuestro libro? —Mati acababa de entrar.

—¡Hola, Mati! —la saludaron los niños a la vez.

—Estamos leyendo lo del principio del palomar –añadió Ven.

—Ah, sí –dijo ella –. Eso os gustó mucho, ¿verdad?

—Sí –aceptó el pequeño –, pero nos dijiste que si teníamos 10 palomas y 3 palomares, en uno de ellos habría menos de 4 palomas, ¿no?

—Ajá –asintió la pelirroja.

—Pero, Mati –siguió Ven –, pueden haber 2 palomares con menos de 4 palomas, por ejemplo, si tienen 3, 3 y 4, ¿no?

—Naturalmente –confirmó ella –. El principio del palomar nos asegura que si hay más palomas que palomares, en alguno de los palomares hay más de una paloma. En nuestro caso, además, podemos deducir que, al menos, en uno de ellos el número de palomas no puede ser mayor que 10/3, porque si el número de palomas en los 3 es mayor que 10/3, el número total de palomas es mayor que 10. Como 10/3 es 3,33333…, no puede haber 4 palomas o más en los 3 palomares y , por eso, en uno de ellos hay, como máximo 3. Pero, naturalmente, puede que haya menos de 4 en 2 de los palomares.

—Aaaaaaaah, vaaaaaaaaaaale –aceptó finalmente Ven.

—Es lo que yo te estaba explicando, Ven –dijo Sal con cara de interesante.

—Pero, vamos a ver, gafotas, no me los estabas contando bien –se enfadó un poco Ven -. Me parece que tú tampoco lo habías entendido muy bien…

—Anda que no… –se defendió el mayor.

—Ya te digo –insistió su hermano –, contigo no me estaba enterando…

—Porque no me estabas prestando atención… —replicó Sal, Gauss se fue a su rincón como si no fuera con él, ya sabía lo que venía.

—¿Cómo que no … —empezó a decir Ven cada vez más enfadado.

—¿Sabes, Mati? —intentó decir el gafotas.

—Eso, y ahora me interrumpes –Ven estaba cada vez más excitado –. Claro, como soy el pequeño no importa lo que tenía que decir.

—¿Qué querías decir, Ven? —preguntó Mati.

—Nada, que te lo diga Sal, que él ya lo sabe y por eso me ha interrumpido –espetó Ven muy digno e indignado.

La situación se ponía cada vez más tensa. Mati dijo de pronto:

—¿Queréis que os cuente cosas muy chulas que se pueden deducir del principio del palomar?

—¡Sí! —dijo Sal entusiasmado.

—¿Ven? —preguntó Mati al pequeño.

—Bueno… —dijo él aún indignado.

—Por ejemplo, en Barcelona hay seguro 2 personas –dijo la gafotas –que tienen exactamente el mismo número de pelos en la cabeza.

Los niños se quedaron mudos mirando a Mati. Gauss resopló, no estaban muy seguros por qué.

—¿Cómo lo sabes, Mati? —preguntó el gafotas.

—Ya verás –dijo ella –. El ser humano suele tener en el cuero cabelludo como máximo, 150000 pelos. En Barcelona viven 1620943 personas. Si a cada una le asignamos un número, correspondiente al número de pelos que tienen en la cabeza, como esos números oscilarán entre 0 y 150000, y hay 1620943 números, alguno de ellos tiene que repetirse. Hay más personas que números distintos disponibles.

—No me entero… —dijo Ven con penita.

—Imaginaos que ponemos 150001 urnas –dijo Mati –, cada una de ellas etiquetada con un número desde el 0 hasta el 150000. Cada habitante de Barcelona escribe su nombre en una papeleta y la deposita en la urna que tiene el número correspondiente al número de pelos que tiene en la cabeza. Como hay más habitantes de Barcelona que urnas, en alguna de las urnas hay, al menos, 2 papeletas, que corresponden a 2 habitantes de Barcelona con el mismo número de pelos en la cabeza.

—¡Toma! ¡Claro! —se sorprendió Ven. Sal sonrió y se subió las gafotas con un dedo.

—¿Veis? —siguió ella –Ya conocéis otra consecuencia del principio del palomar.

—¿Nos cuentas otra? —pidió Sal.

—A ver… —Mati puso cara de pensar muy fuerte –. En cualquier reunión de personas, hay 2 personas que han estrechado la mano al mismo número de asistentes a dicha reunión.

—¿Por qué? —preguntó el pequeño.

—Pensemos en una reunión de, no sé, 20 personas, ¿os parece? —preguntó la pelirroja.

Los niños asintieron con la cabeza.

—Cada persona puede saludar desde 0 a 19 personas, ¿no? Desde no saludar a nadie hasta saludar a todos —volvió a preguntar a los niños.

Ellos volvieron a asentir con la cabeza. Gauss se rascó.

—Le asignamos a cada persona un número –siguió Mati –, el número de personas a las que ha saludado. No pueden haber a la vez una persona que tenga el número 0 y otra el número 19, porque eso significa que la primera, la del 0, no saludó a nadie, pero que la segunda, la de 19, había saludado a todos, incluido el del 0. Así que los números que asignamos van o de 0 a 18, o de 1 a 19.

Los niños volvieron a asentir fuertemente con la cabeza. Gauss bostezó, es un perro con pocas inquietudes.

—Por lo tanto –siguió ella –, tenemos 20 personas y solo 19 números para asignarles. Al menos, tendremos que repetir uno de ellos y habrá 2 personas que tendrán asignados el mismo número, y por lo tanto, que habrán saludado al mismo número de asistentes a la reunión.

—¡Toma, toma, toma! ¡Cómo mola! —a Ven se le estaba pasando el enfado.

—¡Otro! —pidió Sal entusiasmado.

—Venga –anunció Mati –, si colocamos los números naturales del 1 al 10 dispuestos en un círculo, en el orden que queramos, siempre hay tres consecutivos en ese círculo que suman 17 o más de 17.

—Sí, hombre… —dudó el pequeño.

—Dejadme que os lo demuestre –pidió Mati con un guiño –. Escogemos la posición de los números en el círculo, ¿lo queréis hacer vosotros?

—¡Sí! —dijeron los hermanos a la vez y dibujaron en la pizarra de Mati:

—¿Cuánto suman esos números? —les preguntó.

—Espera, lo sabemos –dijo Sal –, nos contaste cómo los calculó Gauss de pequeño.

Gauss ladró haciéndose el importante.

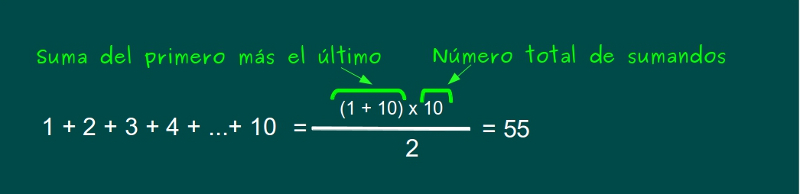
—Eso es, chicos, 55 -dijo Mati –, muy bien. Ahora, escribimos al lado otros 10 circulitos, pero en el lugar de cada número, pondremos la suma del número correspondiente con su anterior y posterior. Por ejemplo, donde está el 1, ponemos 1 más su anterior en la rueda, 4, y más su posterior en la rueda, el 8. Esto es, donde está el 1 en la rueda de la derecha, ponemos 13 en la rueda de la izquierda, el resultado de 1 más 4 y más 8. Vamos a hacerlo con todos

—Ahora nos fijamos –siguió ella –, que los números de la rueda de la derecha suman 165, el triple de 55, porque hemos contado cada número 3 veces: en su casilla, en la de su anterior, y en la de su posterior.

Los niños asintieron, Gauss fingió toser reclamando un poco de atención y Mati continuó:

—Como en casa circulito de la rueda de la derecha, los números son naturales, sin decimales, al menos uno de ellos, debe ser 17 o mayor, por el principio del palomar. Ese circulito corresponde a 3 números consecutivos que suman 17 o más.

—¿Por qué, Mati? —preguntó el gafotas.

—Porque si los 10 circulitos tuviesen un número natural menor que 17 –les dijo –, como mucho sumarían todos 160, si todos fueran 16, y tienen que sumar 165.

—¡Es chulísimo! —gritó Sal —¡Chulísimo!

—¡Otro, otro! —pidió Ven obligando a Gauss a bailar sobre 2 patas.

—Venga, va. Si escogemos 7 números del 1 al 11 -anunció la pelirroja –, dos de ellos suman 12.

—¿Nos los explicas? —pidió Sal con los ojos de par en par.

—Claro –respondió Mati –, elegimos nuestros 7 números del 1 al 11. Ahora vamos a colocarnos en unas cajitas muy especiales. En la primera caja solo podemos guardar el 1 y el 11, en la segunda solo el 2 y el 10, en la tercera el 3 y el 9, en la cuarta el 4 y el 8, en la quinta el 5 y el 7, y en la sexta el 6.

—Como tenemos que guardar 7 números y hay seis cajas –continuó ella —, en una de las cajas hay 2. Esos son los que suman 12.

—¡Mooooooooooooooola! —gritó Ven.

—Otro, por favor –dijo Sal.

—El último –anunció Mati –: si en una pelota dibujáis con un rotulador 5 puntos, 4 de ellos estarán en una de las mitades de la pelota. Si un punto está sobre el círculo que divide a la pelota por la mitad, lo contamos en las dos mitades, ¿vale?

—Ja –dijo Ven desconfiado–, dame una pelota, ya verás…

—No puedes, Ven –dijo Mati –. Te explicaré por qué. Dibujamos los dos primeros puntos, esos nos servirán para dividir la pelota en 2 mitades.

—¿Cómo se divide en 2 una pelota con sólo 2 puntos? —preguntó el gafotas.

—La pelota es una esfera –les explicó –, si tomamos un plano, una cartulina por ejemplo, que pase por esos 2 puntos y por el centro de la esfera, ese plano cortaría la esfera en 2 mitades iguales, en dos semiesferas.

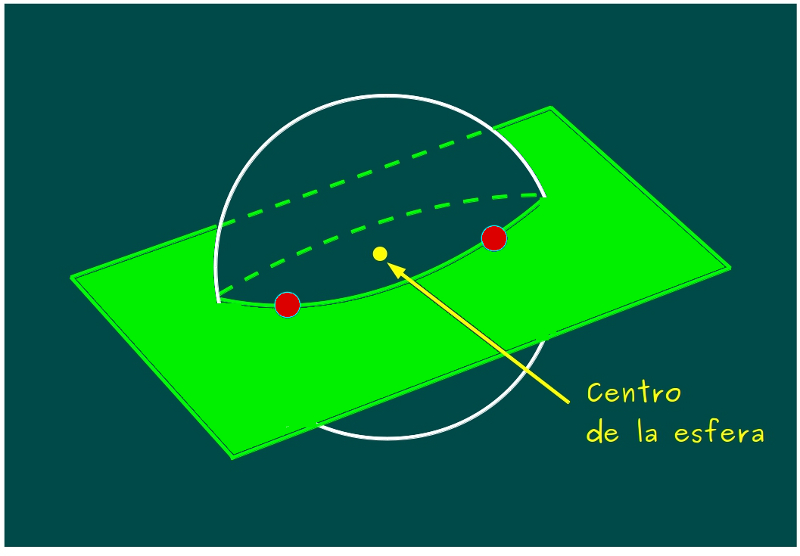
—Pues, ya lo tenéis –anunció ella –, ahora tenéis que distribuir 3 puntos en 2 mitades de la esfera. En una de ellas, tendréis que poner, al menos 2 de ellos, que con los 2 que ya habéis situado, tenéis 4 puntos en la mitad de la pelota.

—¡Impresionante! —exclamó Ven.

—Parecía imposible –dijo Sal que no salía de su asombro.

—Ya os avisé de que el principio del palomar –dijo Mati –tenía muchas consecuencias muy interesantes.

—¿Nos vamos al parque a dar de comer a las palomas? —propuso el gafotas.

—Vale –aceptó Ven –, pero sin Gauss que siempre la lía y me muero de vergüenza…

FIN

¿Habéis visto cuántas cosas tan llamativas se pueden deducir del principio del palomar?

¿Te atreves a deducir tú alguna?

A ver, en una fila de 12 sillas, si se sientan al azar 9 personas siempre hay 3 sillas consecutivas que están ocupadas.

Espero tu razonamiento en los comentarios.

Hasta muy pronto.

MATI