Yo quiero tener 42 amigos

—¿Cuántos amigos llevas ya, Sal?

—Llevo 17 —respondió el gafotas.

—¿Diecisiete? —exclamó Ven muy acalorado —¡No puede ser! No puedes tener más amigos que yo porque tus amigos son mis amigos, y entonces también son amigos de mis amigos…

—Bueno, Ven —interrumpió Sal —, pero si están en mi lista, no pueden estar en la tuya…

—Pero si están en tu lista parece que tú tienes más amigos que yo —siguió protestando el pequeño —, y de eso, nada, ¡tenemos que tener el mismo número de amigos!

—Pero, bueno —Mati acababa de llegar —, eso casi nunca es así, Ven.

—Hola, Mati —la saludó Sal —. Estamos haciendo una lista de amigos para regalarles nuestro libro.

—¿Qué es lo que nunca es así, Mati? —preguntó Ven curioso.

—Hola, chicos —dijo esta —. Lo de que tus amigos tengan tantos amigos como tú.

—No entiendo —dijo Ven torciendo la boca.

—Según la paradoja de la amistad —continuó ella —es probable que tus amigos tengan más amigos que tú…

—Sí, claro —la interrumpió Ven un poco enfadado.

—¿Qué es la paradoja de la amistad, Mati? —preguntó Sal.

—La paradoja de la amistad —les contó —es una propiedad de la Teoría de Grafos…

—¿Grafos como los de Könisberg? —dijo el pequeño.

—Sí, grafos como los que usó Euler para resolver el problema de los puentes de Könisberg —dijo Mati —. Pues esta propiedad viene a decir que es muy probable que nuestros amigos tengan más amigos de los que tenemos nosotros…

—Pero, vamos a ver —interrumpió Ven —, ¡eso es imposible!

—Mirad, —propuso Mati —vamos a hacer una cosa. Suponed que un conjunto de niños lo representamos con este grafo.

—Los niños son los vértices (los puntitos) —continuó —y si dos niños son amigos, los unimos por una arista (una línea). Como podéis ver hay algunos que son amigos de muchos y otros de muy pocos o de uno solamente.

—-Pobres, ¿por qué no los quiere nadie? —preguntó Ven con cara muy preocupada.

—No, Ven no te preocupes —lo tranquilizó ella —, igual es que los que tienen pocos amigos es que acaban de llegar a esa ciudad o, incluso, que son de otra ciudad. Pensad que si representamos la clase de Ot (que está en Barcelona) y a vosotros, en vuestro caso solo conocéis a Ot.

—Ah, claro… —aceptó el pequeño.

— Ahora vamos a contar cuántos amigos tiene cada uno —les propuso —. Escribimos una tabla con 3 columnas, en la primera ponemos la letra que representa cada niño; en la segunda cuántos amigos tiene y también las letras que representan a cada un o de sus amigo. Junto a cada letra, entre paréntesis, escribimos cuántos amigos tiene cada uno de ellos. En la tercera columna, escribimos la media de amigos de sus amigos.

—Uff, qué complicado… —de nuevo, era Ven el que intervenía mientras miraba a la gafotas con el ceño fruncido.

—Pero, Ven —le dijo su hermano —, Mati nos enseñó a calcular la media, ¿no lo recuerdas?

—Además, ya verás, Ven, —le dijo Mati —no es tan complicado. Mira: escribimos la primera fila y verás como es más simple de lo que parece.

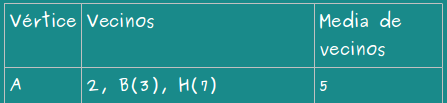
—Para el vértice A —les contó —, miramos en el grafo y vemos que tiene 2 amigos…

—¡*B* y H! —gritó Ven.

—Tenemos además que B tiene 3 amigos (los que ponemos entre paréntesis) y que H tiene 7 —añadió la pelirroja.

—Ajá, ahor alo veo claro… —dijo el pequeño teatrero.

—Para finalizar —continuó ella —, en la última columna hemos escrito la media entre los 3 amigos de B y los 7 de H que es…

—¡¡5!! —gritaron los dos hermanos al unísono. Hasta Gauss dio un ladrido que sonó casi como 5.

—Muy bien chicos, os veo muy despiertos y tú también Gauss— dijo la pelirroja mientras acariciaba la nuca de la mascota.

—Por favor, Mati —solicitó el pequeño —,déjame que acabe yo la tabla, que ya sabes que me encantan esas cosas.

—Claro que sí, cielo —le respondió.

Con la ayuda de Sal, al cabo de un rato, Ven había completado perfectamente la tabla con los datos correspondientes a cada vértice:

—Ahora vamos a observar —les propuso —en cuántas filas el vértice correspondiente (a esa fila) tiene más amigos que la media de amigos de sus amigos.

Los niños miraron durante un rato la pizarrra, Gauss también, sus cosas, ya sabéis…

—Solo en dos: para G y para H —dijo con seguridad Sal.

—Efectivamente, Sal —confirmó ella — Así que podemos decir que, en este grupo, hay 11 niños que tienen menos amigos que sus amigos y solo 2 que tienen más. Es más, si calculamos la media de amigos en todo el grupo (la media del primera dato de la segunda columna), sale 2,5, mientras que la media de amigos de los amigos (en la tercera columna) es de 4,2.

—Es extraño… —dijo Ven pensativo.

—¿Y eso ocurre siempre, Mati? —preguntó el gafotas con cara pensativa.

—Sí, siempre y cuando tengamos una variación en el número de amigos de cada cual dentro del grupo —respondió ella — Esto es: que no todos tengan el mismo número de amigos. Esto es lo que se conoce como la paradoja de la amistad: “en promedio, la gente tiene menos amigos que sus amigos”. Pero lo curioso es que esta paradoja se ha utilizado para cuestiones muy prácticas. Ya contamos alguna para el control de enfermedades..

—Sí, es cierto —dijo Ven, con carita compungida —, pero te tengo que confesar algo, Mati: no lo entendí muy bien…

—Pero si estaba muy claro —respondió Sal, haciéndose el interesante.

—¡Ah!, ¿sí? Venga explícalo tú, listorro —replicó el pequeño al que le solían molestar ese tipo de intervenciones de su hermano.

—Pues… Esto… —dudó el gafotas.

—¡Ja! ¿Ves? Tú tampoco te has enterado.

—Bueno, bueno, bueno —medió Mati—, ya sabéis que no me gustan estas discusiones. Voy a tratar de daros un ejemplo: me contasteis que hace tiempo en vuestro cole hubo piojos.

—Sí, mamá se puso muy pesada todos los días mirándonos la cabeza sin parar —respondió Sal, al que la intervención de Mati había salvado en una discusión sin salida con su hermano.

—Es normal, esas cosas es mejor atajarlas pronto —dijo Mati —, pero conviene saber cuándo van a aparecer para no desatar la alarma entre los padres y evitar que estén todo el día mirando las cabezas sin parar.

—Y eso, ¿cómo puede hacerse? —preguntó de nuevo Sal.

—Para tratar de predecir este tipo de cosas, en ciencia lo que se suele hacer es probar con una muestra —respondió la pelirroja.

—¿Una muestra? —esta vez el que intervino con cara extrañada fue Ven.

—Sí, si en vuestro cole hay unos 450 niños —les dijo —, podemos escoger un 10% al azar que nos sirvan de muestra

—¡45!

—Muy bien, Ven —dijo ella —. Examinamos esos 45 cada cierto tiempo y no pedimos la intervención de los padres hasta que alguno de ellos no tengan “visitantes extraños”. Pero hay una estrategia mejor: escogemos 45 al azar…

—Eso es lo mismo que antes.

—Espera Ven, no te precipites —lo calmó Mati —. Como decía: escogemos 45 niños al azar y ahora les pedimos que cada uno escriba el nombre de un amigo y en vez de examinar a los 45 escogidos inicialmente, nos dedicaremos a examinar periódicamente a los amigos señalados.

—Y, ¿qué ganamos con ello? —preguntó Sal.

—Ya verás —anunció la pelirroja co voz misteriosa —: ya sabemos que los piojos se transmiten por cercanía, así que si un niño tiene “visitantes” es fácil que se los pase a sus amigos. Pero sabemos por la paradoja de la amistad que la media de amigos de los 45 escogidos al azar está por debajo de la media de amigos de sus amigos. Entonces, cuando les pedimos que escriban cada uno el nombre de un amigo, estamos escogiendo una muestra que tiene, de media, más amigos y, por tanto, nos permitirá controlar mejor qué está ocurriendo.

—¡Ah! ¡Qué interesante! —dijo Sal pensativamente.

—¿Verdad que sí, Sal? —le preguntó ella.

—Y, ¿no podrías poner otro ejemplo? Que me están entrando picores de tanto hablar de piojos —repuso Ven.

—Es verdad cielo, a mi también me pasa. Se pueden poner muchos ejemplos. Pero digamos que esta propiedad de los grafos está relacionada con otras muchas de estadística y que hay que tener en cuenta o para obtener mejores resultados y conseguir una muestra más representativa “más buena”, como en el ejemplo de los…, bichitos que acabamos de contar —dijo Mati mirando de reojo a Ven .

—Más buena ¿por qué? —preguntó este.

—Porque observa que si escogemos 45 niños al azar, eso es una muestra del colegio, mientras que si a estos 45 niños les pedimos que escriban el nombre de un amigo a cada uno, lo que estamos consiguiendo es una muestra entre los más populares del colegio y por ello, al tener más amigos, están más expuestos. Pero, también podemos usar este tipo de muestra para otras cosas. Por ejemplo, Ven, tú estás interesadísimo en los cromos de futbolistas ¿verdad?

—Sí, claro, pero todos en el colegio lo están —dijo el pequeño.

—Pues —continuó la pelirroja —podemos usar la paradoja de la amistad para completar mejor un álbum.

—¿Sí? —preguntó Ven con los ojos como platos.

—Sí, supongo que cuando tienes cromos repetidos intentas cambiarlos y lo primero que haces es probar entre tus amigos, ¿no? —dijo ella.

—Sí —repuso el pequeño que ya empezaba a vislumbrar que su “táctica” no era la más adecuada.

—Pero eso tiene el problema de que siempre intentas cambiar tus cromos entre los mismos —siguió Mati —. Mejor sería si en el recreo te acercas a unos cuantos niños al azar y tratas de cambiar cromos con ellos y aún mejor si te acercas a esos niños al azar y les pides que te acerquen a uno de sus amigos, porque así estarás buscando a los más populares que, al tener más contactos, tienen más posibilidades de haber conseguido ese cromo que te falta y que es tan deseado por ti.

—¡Toma, toma, toma! ¡Me encanta la paradoja de la amistad! —exclamó Ven.

—Pero hay que tener cuidado —intervino Mati —, porque, a veces las muestras por esta misma razón, nos pueden engañar y dar resultados que nos alejen de la realidad. Ya pusimos un par de ejemplos el otro día..

—Sí, contabas algo de un gimnasio —dijo Sal.

—Eso es: cuando alguien lleva un tiempo en un gimnasio se puede desmoralizar porque ve que la mayoría de la gente lo hace mejor y se puede llegar a pensar que a los otros le aprovecha mejor —les contó Mati —. Pero hemos de pensar que, si miramos a nuestro alrededor en el momento que estamos en el gimnasio, estamos extrayendo una muestra de la gente que está apuntada al gimnasio y esa muestra está, como dicen los estadísticos, sesgada.

—Ses…, ¿qué? —Preguntó Ven.

—Sesgada —repitió la gafotas —, lo que quiere decir que no representa bien a todos los que están apuntados al gimnasio, ya que los que vemos en cada momento son los que están en el gimnasio y es fácil que veamos más a menudo a aquellos que pasan muchas horas allí y que, por tanto, estén en muy buena forma.

—Toma, claro… —aceptó finalmente Ven.

—Y ahora —dijo Mati cambiando el tono —, ¿queréis que os eche una mano con vuestra lista de amigos?

—Yo ya casi tengo la mía… —respondió Sal.

—Yo tengo muy pocos aún, Mati —añadió Ven con penita —. Solo tengo apuntados 14.

—Pero, Ven —dijo la pelirroja —-, 14 libros ya son muchos libros… ¿¿cuántos amigos quieres tener??

—42 —contestó el pequeño sin inmutarse.

—¿¿*42*?? —exclamaron a la vez Sal y Mati.

—Naturalmente —respondió el aludido sin apenas inmutarse —, el sentido de la vida, el universo y todo lo demás

Mati y Sal soltaron una carcajada con la ocurrencia de Ven. Gauss recordó que había tomado más galletas de la cuenta esa semana…

FIN