7 puentes para un solo paseo

—¿Falta mucho, Mati? Estoy cansado…

Ven casi no puede andar después de pasar el día en el parque de atracciones.

—Yo no puedo más… —añadió Sal que casi ya no podía con sus gafitas, mientras agarraba a su loro al que habían decidido llamarle Fermat porque hablar, no había demostrado que pudiese hablar.

—Sólo hay que cruzar el puente y llegamos. ¡Ánimo, piratas!

—Es que este puente es tan largo…

—Ven tiene razón, Mati, es larguísimo.

Mati, viendo la moral de su tropa derribarse por momentos, le pregunta:

—¿Sabéis cómo se llama este puente?

—Barqueta —dijo Sal casi sin resuello.

—Parece un canasto.

—Sí, es verdad —dijo Mati sonriendo.

—A mí me gusta más el del Alamillo…

—¿Cuántos puentes hay en Sevilla, Mati?

—Uy, pues sólo sobre la dársena del Guadalquivir hay 9…

—Contando el del Quinto Centenario, ¿no?

—Bueno, ése está sobre el brazo vivo del río, y no está en la ciudad… Oye, por cierto, os voy a contar un acertijo sobre puentes y descansamos un rato.

Los pequeños, sin decir nada, se dejaron caer sentaditos en el suelo.

—Hace mucho tiempo, en el siglo XVIII, en una ciudad llamada, por entonces, Könisberg, pasaba un río, Pregel, que dividía a la ciudad en cuatro partes…

—¿Cómo puede ser eso, Mati? —interrumpió Sal mirando por encima de las gafotas.

—Pues porque tenía esta forma, a ver:

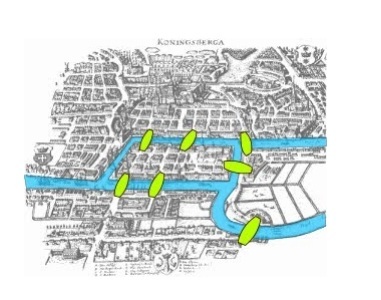
—En esos tiempos, alguien formuló la siguiente pregunta: «¿Es posible, comenzando en cualquier sitio de la ciudad de Könisberg, elegir un camino que nos permita pasar una única vez por cada uno de los siete puentes sobre el río Pregel?»

—¿Andando? —preguntó Ven despavorido.

Mati soltó una carcajada.

—Bueno, eso da igual, en bici, si quieres —le respondió la pelirroja.

—¿Existían las bicis? —quiso saber el gafotas.

—Pues no, porque el precursor de la bicicleta fue un señor inventor alemán, Karl von Drais, y eso fue ya en el siglo XIX —les contó —Pero bueno, como estáis cansaditos, lo pensaremos en bici. ¿Qué creéis? ¿Se puede?

Los niños se quedaron un rato pensando, garabateando el mapa de Könisberg que les había dado.

—Fijaos en una cosa, si ponemos un punto en cada una de las cuatro partes de la ciudad y una rayita uniendo los puntos, como si fueran los puentes…

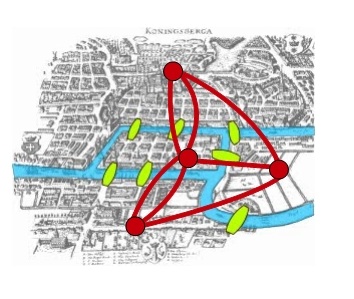
…la pregunta sería si puedo dibujar esto:

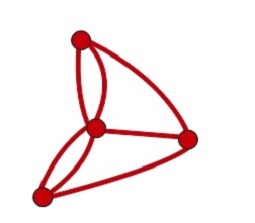
sin levantar el lápiz y sin pasar dos veces por la misma rayita.

Finalmente, Sal sentenció:

—No, no se puede.

—¿Por qué?

—Porque no nos sale —respondió con cara de pícaro sabiendo que eso no era un prueba concluyente para Mati.

—Pues, muy bien, ésa es la respuesta pero no es la explicación. Fue Euler, un matemático muy famoso, el que demostró que, efectivamente, era imposible. Este tipo de dibujos, con puntos y líneas, se llaman grafos. Pues bien, Euler, que era más listo que la mar, demostró que un grafo se puede dibujar empezando en uno de los puntitos pasando por todas las líneas, sin repetir ninguna, sólo si, como mucho, hay dos puntos que tienen un número impar de líneas saliendo de ellos.

—Vamos a ver qué pasa con nuestro grafo. Contaremos cuántas líneas salen de cada punto.

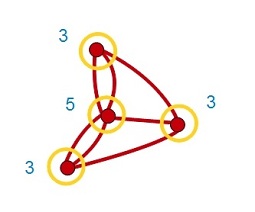
—Todos son impares, Mati —dijo Ven con tristeza.

—Entonces, no se puede, porque no puede haber más de 2. ¿Y éste? ¿Se puede?

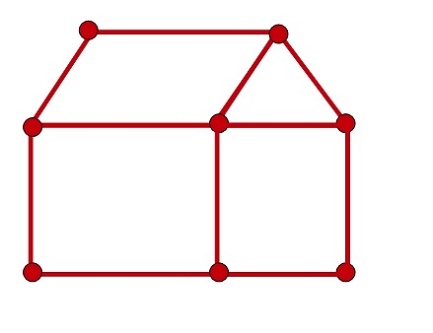
—Bueno, tampoco, porque tiene cuatro puntos con un número impar de líneas —aseguró, muy acertadamente Sal.

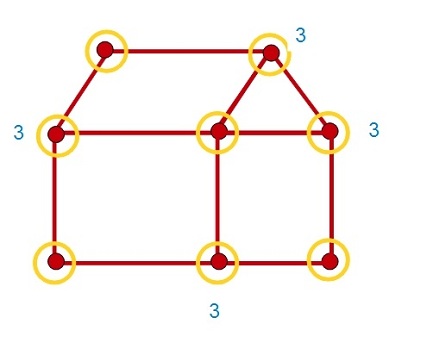
—Muy bien, Sal. En realidad, no hace falta contar las líneas que salen de cada punto, en el momento en que encuentras tres puntos con un número impar de ellas, ya has terminado.

—Otro, Mati, ¡otro! —pidió entusiasmado Ven

—A ver éste:

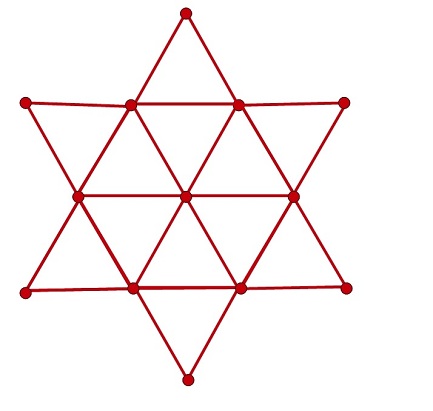
Los niños se pusieron manos a la obra a contar las líneas que salían de cada vértice, finalmente el pequeño gritó:

—¡Tampoco! ¡He encontrado ya tres puntos con 5!

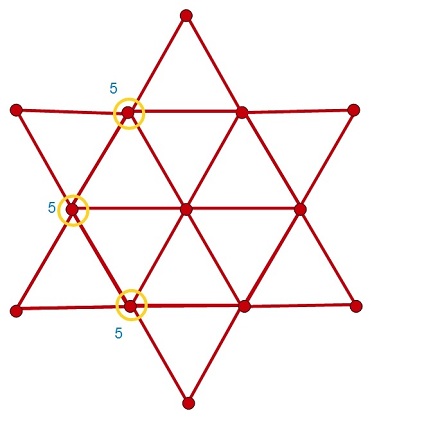
—Muy bien, Ven. Ahora probemos, con otro, ¿se podrá dibujar sin levantar el lápiz y sin pintar ninguna rayita dos veces?

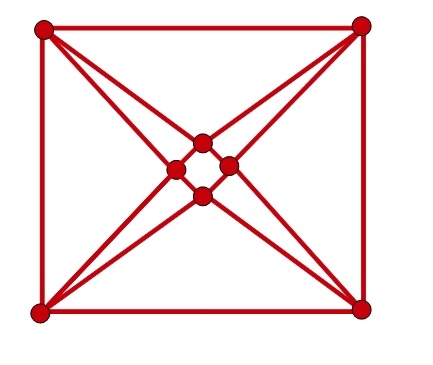
—¡Éste sí! —Sal estaba sonriendo satisfecho—; ¡todos son pares!

—Exacto. A ver si sois capaces de dibujarlo sin repetir líneas y sin levantar el lápiz.

Los dos hermanos se pusieron manos a la obra y tras algún que otro intento fallido, encontraron la forma de hacerlo como les había pedido su amiga Mati.

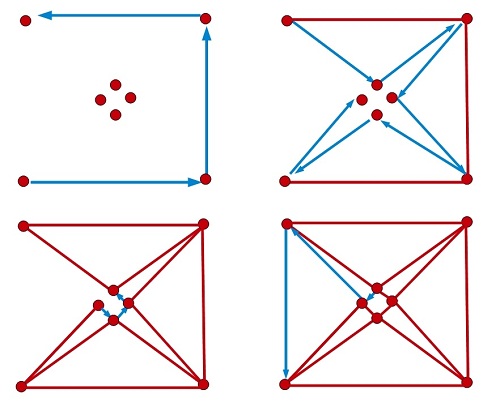
—Muy bien, piratas. Estoy orgullosa de vosotros. Otro más.

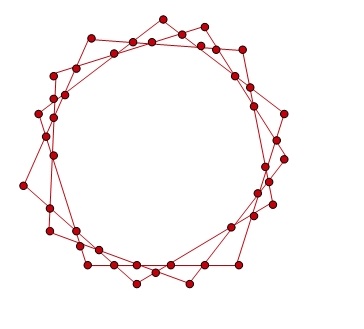
—Todos pares —dijo Ven muy orgulloso.

—Pues, nada, intentad hacerlo —Mati les guiñó un ojo.

—¿Ahora, Mati? Estoy muy cansado.

Mati acarició la carita de los dos pequeños mientras que reiniciaban el camino a casa.

El problema de los puentes de Könisberg es famoso por ser el origen de una rama de las matemáticas conocida como Teoría de Grafos. Efectivamente, fue Euler el matemático que lo resolvió y por eso, a los caminos que recorren todas las aristas (líneas) del grafo, sin repetir ninguna, se les llama caminos eulerianos.

Si queréis profundizar más en este problema os recomiendo esta entrada en Gaussianos.

Cuando se planteó el problema de los puentes, Könisberg formaba parte de Prusia Oriental. Actualmente la ciudad pertenece a Rusia y se llama Kaliningrado. De los 7 puentes originales, dos fueron destruidos durante la Segunda Guerra Mundial. Otros dos de los puentes, se derribaron y reemplazaron por otros más modernos en el mismo emplazamiento. Con lo que, actualmente, sólo quedan 5 puentes (de los originales) en la ciudad como se ven en la figura, marcados en amarillo.

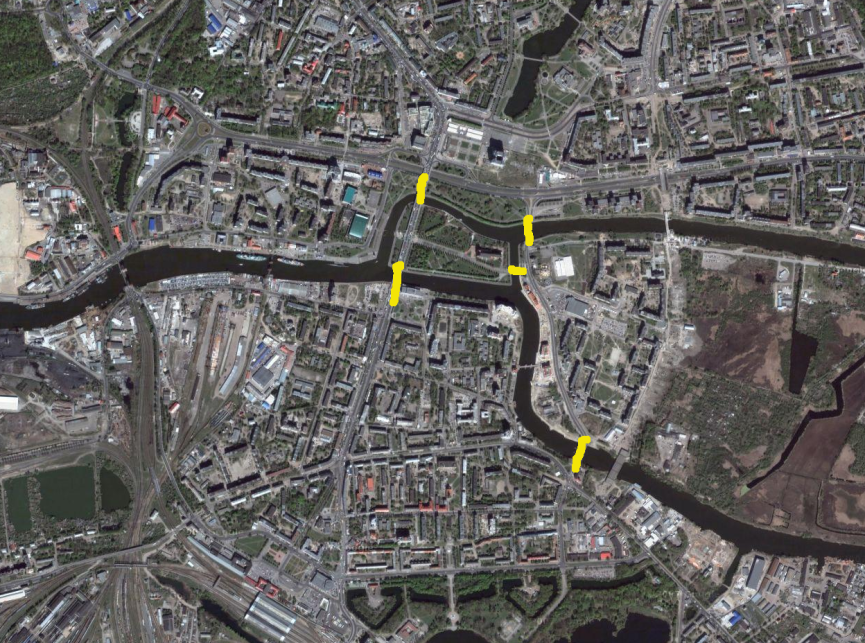
Y la pregunta es: y con esos 5 puentes, ¿se puede hacer un recorrido comenzando y terminando en el mismo punto de la ciudad y pasando una y sólo una vez por cada puente?