18 monedas de chocolate

—Fuencarral es mía, así que, ¡paga, paga, paga! —gritó Sal con entusiasmo.

— Otra vez, ¡qué rabia! —protestó Ven enfurruñado.

—Lo siento, Ven, el juego es el juego. Peor es si caes en el Paseo del Prado…

—Toma, pesado.

Sal se dispuso a contar el dinero que su hermano pequeño le había entregado.

—¡Qué morro tienes, Ven! ¡Éste lo has pintado tú!

—¿Yo? No, de verdad —contestó el pequeño sin mirar de frente a su hermano.

—No disimules, se nota perfectamente ¡Los números están torcidos! ¡Es falso!

—Pero bueno…¿qué pasa aquí? —Mati acababa de llegar.

—¡Hola, Mati! —saludó Ven con alegría mientras la abrazaba para huir de la mirada
inquisidora de su hermano.

—Hola, Mati —saludó el gafotas —Ven ha intentado pagarme con dinero falso,
¡es un tramposo! —terminó diciendo mientras se acercaba a abrazar a su amiga pelirroja.

—Pero si todo el dinero del monopoly es falso, ¿qué te crees? —intentó defenderse
desesperadamente Ven .

—Ya, pero…bueno, el que tú has pintado es falsísimo, ¡peor que falso! —las gafas de
Sal se resbalaron por su naricilla.

—Uy, ¿sabéis qué? —interrumpió Mati —Me habéis recordado un acertijo sobre monedas buenas y falsas —la gafotas hizo una pausa dramática —Pero, probablemente, es un poco complicado para vosotros.

—¿Cómo es? —preguntó el gafotas mientras se las colocaba de nuevo en su sitio y se le iluminaban los ojillos.

—¡Sí, sí, sí! —gritaba Ven nervioso — Cuéntanoslo, por fi, por fi, por fi…

—Está bien — contestó satisfecha la pelirroja.

Los niños se sentaron en el suelo. Gauss se pavoneó aún un rato más con su sombrero.

—Ya veréis. Tenemos 10 amiguitos que llevan 10 monedas cada uno en sus bolsillos. 9 de ellos tienen monedas auténticas, que sabemos que pesan 10 gramos, y uno de ellos tiene sólo monedas falsas que pesan 11 gramos…

—Tan falsas como el billete de Ven…—masculló Sal. Su hermano le sacó la lengua con disimulo.

—La pregunta es —continuó Mati — ¿Podéis detectar quién de ellos tiene sólo monedas falsas pesando sólo una vez?

Lo niños se quedaron muy serios pensando, Gauss siguió jugando con su bastón.

—Imposible, Mati —Ven fue el primero en rendirse.

—¿Sal? —dijo ella.

—No se me ocurre, Mati —terminó reconociendo Sal con pena.

—Pues, veréis. Numeramos a los amiguitos del 1 al 10. Y le pedimos 1 moneda al primero, 2 monedas al segundo, 3 al tercero, 4 al cuarto…Y así, sucesivamente, hasta el décimo que le pedimos las 10. ¿Cuántas monedas tendremos?

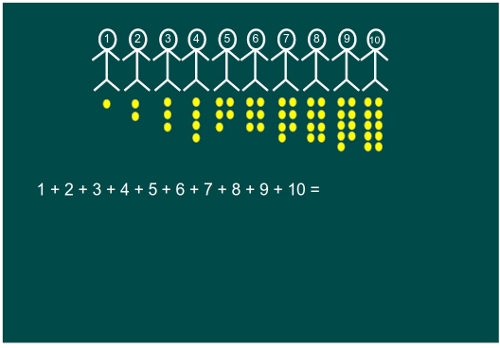
—¡Toma, toma, toma! Eso lo sé, lo descubrió Gauss cuando pequeño, nos lo contaste. Era 11, el primero más el último, multiplicado por la mitad de los niños, 5.

—55 —terminó de decir Sal.

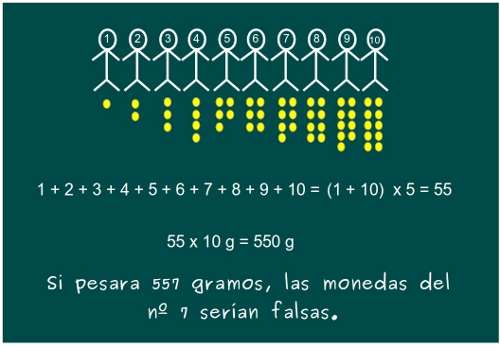
—¡Muy bien, chicos! —dijo Mati orgullosa —Si las 55 monedas fueran auténticas, deberían pesar ¿cuánto?

—¡550! —gritó Ven asustando al pobre Gauss.

—Pues bien, si pesamos y tenemos 557 gramos… —dijo la gafotas.

—¡El niño número 7 tiene las monedas falsas! —concluyó Sal con otro grito, asustando de nuevo a la pobre mascota.

—¡Tomaaaaaa! ¡Cómo mola, Mati! —el pequeño Ven tenía los ojos como platos.

—¿Otro, chicos?

—¡Sí! —gritaron al unísono los dos hermanos.

—Ahora tenemos 5 monedas, y sabemos que una de ellas es falsa, pero no sabemos cuál, sólo que pesa distinto de las demás. Además, tenemos una moneda aparte que sabemos que es auténtica. Ahora usaremos una balanza de platillos, que se inclina hacia el platillo que pesa más, o se queda en equilibrio si los dos platillos pesan lo mismos, ¿me explico?

—Perfectamente —contestó el gafotas.

—Tenéis que detectar la moneda falsa…

—Qué fácil, Mati, pones en un platillo cada una de las 5 monedas, una cada vez, y en el otro platillo, la moneda auténtica. Ya está —Ven sonrío triunfalista.

—Muy bien, pero sólo te dejaré usar la balanza 2 veces —dijo Mati.

—Pues vaya…—protestó el pequeño.

—Si pones 3 y 3 en cada platillo…. —mascullaba Sal —…si el platillo con la buena pesa menos…en el otro hay una que pesa de más…

—O en el platillo de la buena hay una que pese menos, ¿no, Sal? —preguntó su hermanito.

—Eso es verdad…o sea que no sirve de nada esa pesada —concluyó Sal muy serio.

—¿Cómo es, Mati? —la impaciencia de Ven hablaba por él.

—Venga, vale, me rindo —aceptó el gafotas.

—Vamos a coger sólo 3 monedas de las 5 y pesaremos, 2 de ellas en un platillo, y la otra, junto con la auténtica, en el otro platillo.

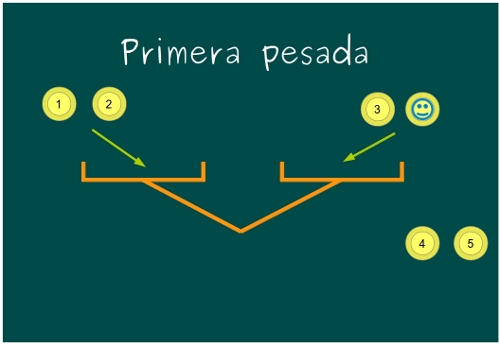
—¿Qué pasa con las otras, Mati? —se preocupó Ven.

—Tranquilo, pequeño, ya verás ¿Qué podríamos adivinar si la balanza se queda en equilibrio?

—¡Que los dos platillos pesan lo mismo! —dijo Ven con alegría.

—¿Que las cuatro monedas que hemos pesado son auténticas? —preguntó el gafotas.

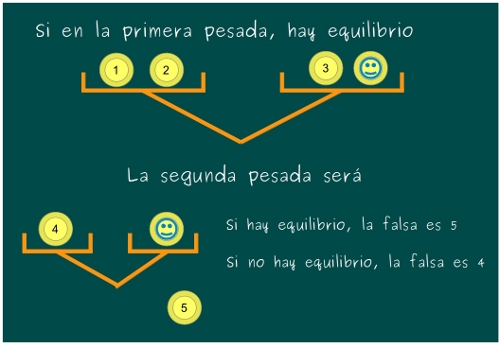
—Exacto, los dos tenéis razón. Hay que buscar la moneda falsa entre la 4 y la 5, y nos queda una pesada. ¿Qué hacemos?

—Pesamos las 4 y la auténtica. Si pesan iguales la falsa es la 5, y si pesan distinto, la falsa es la 4, ¿no, Mati? —Ven miraba nervios a la pelirroja esperando la respuesta de ésta.

—¡Muy bien, Ven, así es!

—¡Toma, toma, toma! ¡Soy un crack! —Ven movía los brazos de arriba a abajo con los puños apretados.

—Eso si en la primera pesada hay equilibrio, pero… —continuó Mati —¿y si la balanza se inclina hacia el platillo que contiene la auténtica?

El gafotas se apresuró a contestar:

—En ese caso, o bien la 1 o bien la 2 es falsa y pesa menos, o bien la 3 es falsa y pesa más.

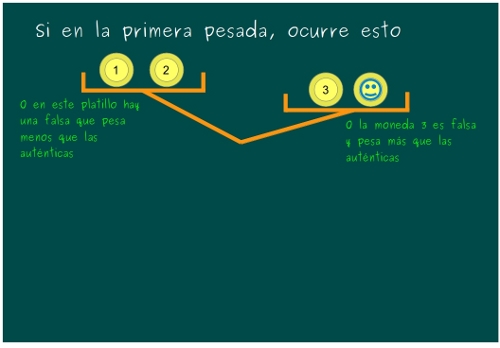
—Bravo, Sal —contestó ella —Nos queda una sola pesada, ¿qué hacemos?

Los niños estuvieron un rato cuchicheando entre ellos, las tripas de Gauss eran la música de fondo. Y es que a nuestro amiguito pensar le da hambre.

—¡¡Lo tenemos, Mati!! —gritó Ven acallando las tripas de su mascota.

—Sí, sólo tienes que pesar la 1 y la 2. Si pesan iguales, la falsa es la 3, que pesa más. Y si no pesan lo mismo, la falsa será la que pese menos, porque sabemos que en ese platillo, si hay una falsa, es más ligera.

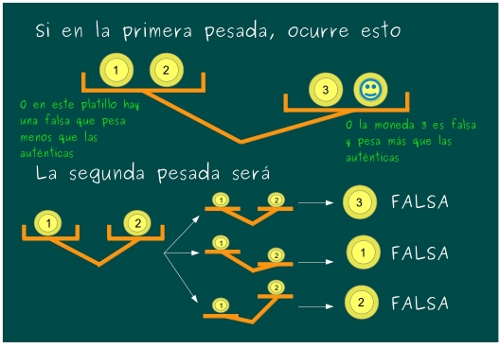
—Pero, bueno… Muy bien, chicos, eso es —Mati revolvió el pelo de los dos niños que se estremecieron de gustito.

—Y si el platillo se inclina al contrario, Mati, se hace igual, pero al revés —el gafotas estaba lanzado.

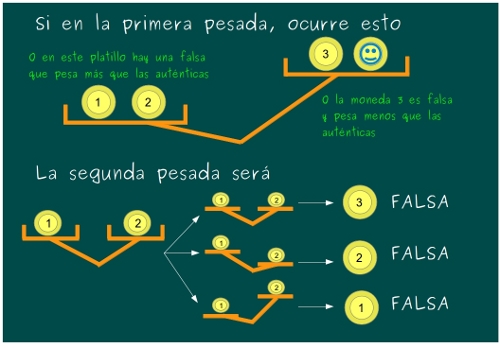
—Exacto. Y pensar que yo pensaba que estos acertijos eran muy complicados para vosotros…

—¡Otro, otro! —pidió el pequeño Ven.

—Bueno, vosotros lo habéis querido —Mati guiñó un ojo y puso voz de presentadora de concurso —Ahora tenemos 12 monedas. Sabemos que una es falsa, porque pesa diferente…

—¿Cuántas pesadas? —quiso saber Sal.

Mati hizo una pausa dramática de silencio mientras miraba a los ojos primero a Sal, luego a Ven, otra vez a Sal, otra vez a Ven… Las orejas de Gauss se pusieron tiesas…

—Tres —dijo la pelirroja con voz de mala, malísima de película —Y quiero saber si la moneda falsa pesa más o menos que la auténtica, ¿eh?

—¿¿Sólo tres?? —preguntó el gafotas sorprendido.

—Es broma, Sal, ¿verdad, Mati?

—No, no es broma —dijo y los miró, cómicamente, desafiante.

Sal y Ven montaron su gabinete de lucha contra el fraude, cuchicheaban en voz baja tratando de resolver el reto propuesto por su amiga gafotas.

—6 y 6 no sirve para nada, porque no sabemos si la falsa pesa más o menos…—razonaba Sal.

—¿Y si ponemos 5 y 5, dejando 2 monedas fuera como antes? —sugirió el pequeño.

—Pero ahora no tenemos moneda auténtica para comparar, Ven.

—Toma, claro, es verdad…

Al cabo de unas cuantos intentos improductivos…

—¿Nos rendimos, Sal?

—Sí, no se me ocurre. Nos rendimos, Mati.

—Éste es un poco más complicado, ¿eh? No os desaniméis. Empezamos con cuatro monedas en cada platillo…

—¡Cachis! Casi lo dijimos… —Ven apretó los labios contrariado.

—Ven, calla, deja hablar a Mati.

— ¿Qué pasa si los 2 platillos pesan lo mismo? —les preguntó.

—Que las 8 son auténticas —dijo Ven

—¡Claro! Y ahora sólo tenemos que buscar entre 4 monedas y además, tenemos 8 auténticas que podemos usar para comparar —los ojos de Sal brillaban como estrellas.

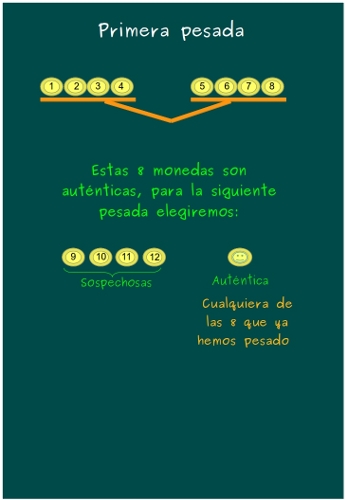
—Eso es, chicos, ¿cómo seguimos?

—Pues no sé… —dudaba Sal —¿La 9 y la 10 en uno, y la 11 y la buena en otro?

—Eso es, Sal ¿Qué sabremos si la balanza queda en equilibrio?

—¡Que la moneda falsa es la 12!

—Muy bien, Ven.

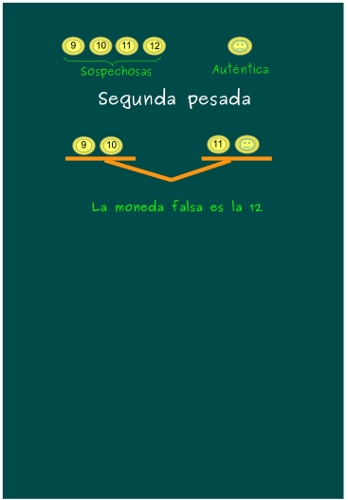
—¡Toma, toma, toma! ¡Y nos sobra una pesada! ¡Mola!

—No, Ven —intervino Sal —Tenemos que saber si la moneda 12 es más ligera o más pesada que la auténtica. Necesitamos la tercera pesada.

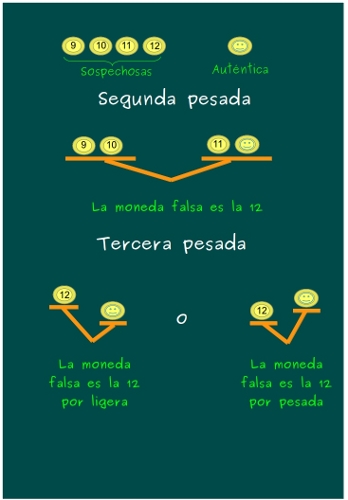
—Tengo que reconocer que estoy maravillada con vuestras deducciones, chicos.

—Es que somos unos buenos detectives…—respondió Ven con cara de pillo.

—Lo sois, sin duda —Mati le guiñó un ojo —Seguimos. Ya sabemos como proceder si la segunda pesada deja la balanza en equilibrio. Pero, ¿y si no la deja? ¿Y si se inclina hacia el platillo con la 9 y la 10?

—Entonces, tenemos dos sospechosas de falsas monedas más pesadas, la 9 y la 10, y una sospechosa de ser más ligera, la 11 —dijo el gafotas.

—¡Pues comparemos la 9 y la 10! —sentenció el pequeño —Si una de ellas pesa más, es la falsa. Y si las 2 pesan iguales, la falsa es la 11 y pesa menos.

Mati sonreía satisfecha mientras ilustraban las posibilidades en la pizarra.

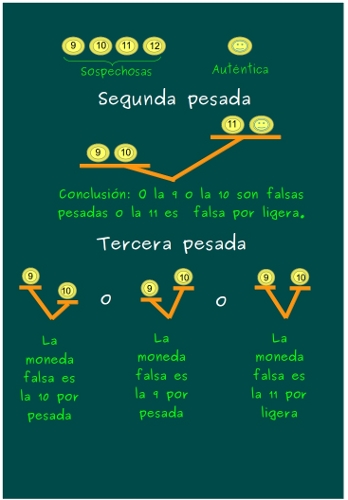
—Mati, ¿puedo intentar hacer yo el esquema en el otro caso? —preguntó el gafotas.

—Claro, ¿por qué no?

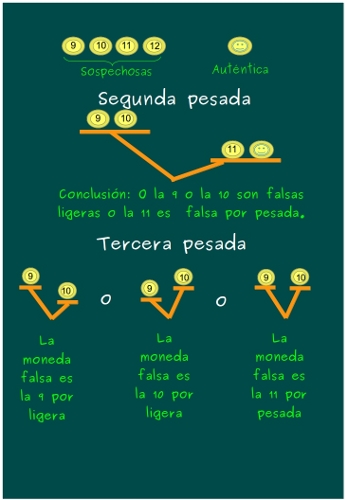
—¡Fantástico! —dijo Mati con orgullo provocando la pelusilla de Gauss —Por lo tanto, si al comparar las 8 primeras monedas, 4 en cada platillo, la balanza se queda en equilibrio, ya lo tenemos.

Los niños sonreían satisfechos, Gauss decidió ir a merodear un rato…

—Vamos a ver cómo proceder si no es así, si al pesar las primeras 8 monedas no hay equilibrio porque, por ejemplo, se inclina hacia el platillo con la 5, la 6, la 7 y la 8.

Sal y Ven arrugaron sus ojillos en actitud de pensar mucho, pero mucho, muchísimo, durante unos segundos.

—Ahora, Mati, tenemos 4 monedas sospechosas de pesar menos y 4 monedas sospechosas de pesar más —empezó diciendo Sal.
—¡Y 4 monedas que sabemos que son auténticas, las 4 que no hemos pesado! —puntualizó su hermanito —Y que podemos usar para comparar.

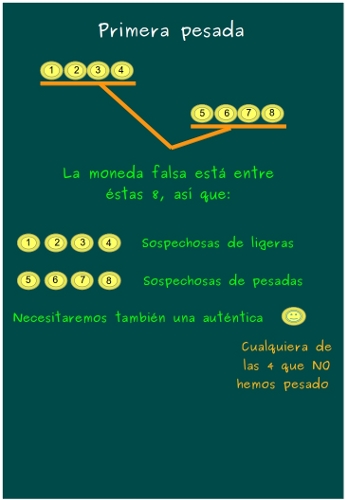
—Eso es ¿Cuál es la segunda pesada, chicos?

El gabinete contra el fraude estuvo dándole vueltas un buen rato, sin encontrar ninguna propuesta que les gustara, aceptando finalmente su rendición.

—Bueno, ésta es un poco más complicada. Os cuento: en un platillo pondremos una sospechosa de ligera, una sospechosa de pesada y la buena; en el otro, 2 sospechosas de ligera y una sospechosa de pesada.

Los niños no dijeron nada, sólo abrieron sus ojos al máximo.

—Si la balanza queda en equiibrio —continuó la gafotas —será porque las 6 son auténticas, sólo quedan 3 sospechosas, la 4, la 7 y la 8.

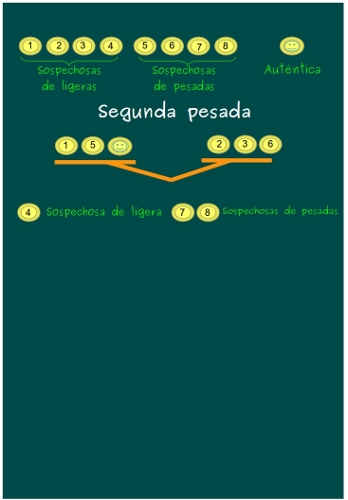
—Entonces, sólo tenemos que comparar las 2 que son sospechosas de falsas por ser más pesadas —Sal no podía disimular su emoción.

—¡¡Toma, toma, toma!! ¡¡Alucinante!! —Ven abrazó a su hermano con tanto ímpetu que las gafotas de Sal cayeron al suelo. Éste las recogió sin poder dejar de sonreír.

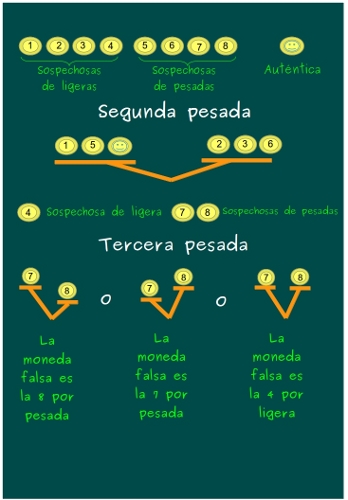
—¿Y si no hay equilibrio? —preguntó una Mati henchida de orgullo de sus amiguitos.

— Las sospechosas serán las sospechosas por pesadas que estén en el platillo más pesado, y las sospechosas por ligeras que estén el platillo que pese menos —explicó Sal.

—Y ahora a comparar las dos sospechosas por ligeras —dijo el pequeño

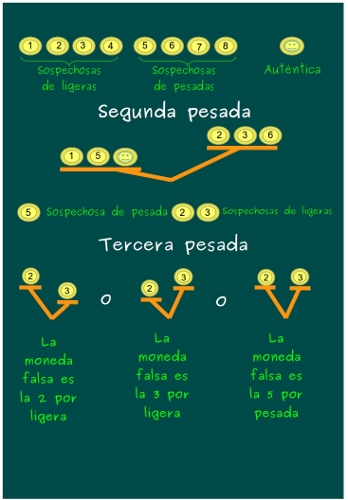
—Vaya, vaya, vaya… Estoy maravillada con vuestras deducciones. Ya casi lo tenéis. Sólo os queda el caso en el que el platillo con la 2, la 3 y la 6 es más pesada que la 1, la 5 y la buena…

Los niños se pusieron mano a la obra terminando de analizar este último caso en la pizarra de Mati

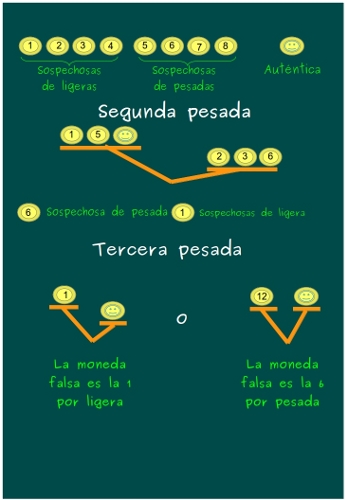
—Ya está, Mati —dijo Sal satisfecho mientras se subía las gafotas con su dedo índice, mientras Ven daba vueltas tapándose la cara con la parte delantera de su camiseta, gritando algo ininteligible.

—Muy bien, chicos, muy, muy bien —dijo Mati —Esto se merece unas monedas, pero de chocolate, ¡os he traído 18! —la pelirroja guiñó un ojo —Pero, ¿dónde las puse yo al llegar? Juraría que las dejé aquí junto al teléfono…

FIN