Porque 8 no es siempre el doble de cuatro

—¿Vamos al jardín a jugar con Gauss? —propuso Sal a su hermano mientras trataba de convencer a su mascota de que se levantara de su camita.

—Hace frío.

—No hace frío —replicó el gafotas mientras se acercaba a la estación meteorológica del salón —Hace 18º fuera, eso no es frío.

—¡Anda que no! Hace la mitad de calor que en verano que hace 36º o más…

—¡Pero el doble que en invierno que hace 9º o menos!

—Bueno, bueno, eso no es exactamente así, caballeros…

—¡Hola, Mati! —saludaron los dos hermanitos con alegría. Gauss se acercó a buscar el achuchón de la pelirroja.

—Hola chicos. Dos cosas. Uno: no hace tanto frío, podemos salir al jardín. Dos: 36º no es el doble de calor de 18º, ni 18º el doble de 9.

—¿Cómo? —protestó Sal —18 × 2 es 36, Mati…

—Si, pero no es necesariamente el doble de temperatura, depende de la escala elegida para medirla.

Sal, Ven y Gauss se quedaron muy serios mirando a la gafotas que continuó:

—Nosotros medimos la temperatura usando grados Celsius, o centígrados, como se les llamó tras la Revolución Francesa, que impuso el sistema métrico decimal. Pero en Estados Unidos y en algún que otro país de América Central, la temperatura se mide en grados Fahrenheit.

—Entonces, en Estados Unidos, ¿no usan los termómetros como nosotros cuando están resfriaditos?

—Naturalmente, pero miden los grados con otra escala, se llama escala Fahrenheit, en honor al físico que la diseñó que tenía ese apellido.

—Supongo que Fahrenheit era estadounidense, ¿no, Mati?

—Pues no, Daniel Gabriel Fahrenheit era alemán, nacido en la ciudad alemana Danzig, que actualmente se llama Gdansk y está en Polonia.

—Y si era alemán, ¿por qué en España no la usamos? ¿Por qué el otro era español?

—¿Quién? ¿Celsius? No, tampoco, era sueco. Propuso una escala para medir la temperatura, después que Fahrenheit por cierto, que iba de 100º a 0º, 100ºC para la temperatura en que se congelaba el agua a nivel del mar y 0ºC para la temperatura en que hierve el agua al mismo nivel.

—¡Al revés, Mati! —dijo Ven con sonrisa pícara

—No, así, en serio. Cuanto más calor hacía, menos temperatura marcaba. Más tarde, otro sueco, Carlos Linneo, fue el que le dio la vuelta al termómetro y lo dejó como lo conocemos ahora: 0ºC temperatura de congelación del agua y 100ºC para la ebullición de la misma.

—Qué curioso…y para Fahrenheit, la temperatura no iba a de 0 a 100.

—Bueno, para Fahrenheit, el 0ºF estaba en el punto de congelación de agua con hielo y cloruro de amonio que no es el mismo punto dónde lo puso Celsius, sino una temperatura mucho más baja aún.

—¡Ay, que lío, Mati!

—Entonces, si nos ponemos malitos en Nueva York, no entenderemos los termómetros —continuó Sal preocupado.

—No, hombre —os enseñaré a transformarlo, ya veréis qué fácil. El agua se congela a 0º C y hierve a 100º C, lo que indica una diferencia de 100º. El agua se congela a 32ºF y hierve a 212º F, lo que indica una diferencia de 180º. Por lo tanto cada grado en la escala Fahrenheit es igual a 100/180 o 5/9 grados en la escala Celsius.

Si tenemos la temperatura en grados centígrados o Celsius, la tenemos que multiplicar por 9, el resultado lo dividimos por 5 y a lo que salga, le sumamos 32. Vamos a transformar en grados Fahrenheit 9, 18 y 36 grados Celsius.

— ¿Veis? Cuando hace 36ºC no es el doble de temperatura de cuando hace 18ºC, porque 96,8ºF no es el doble de 64,4ºF. Luego, depende de la escala con que se mida

—Y si en Estados Unidos hace 36ºF, ¿cuántos grados Celsius serían?

—Vamos a calcularlo

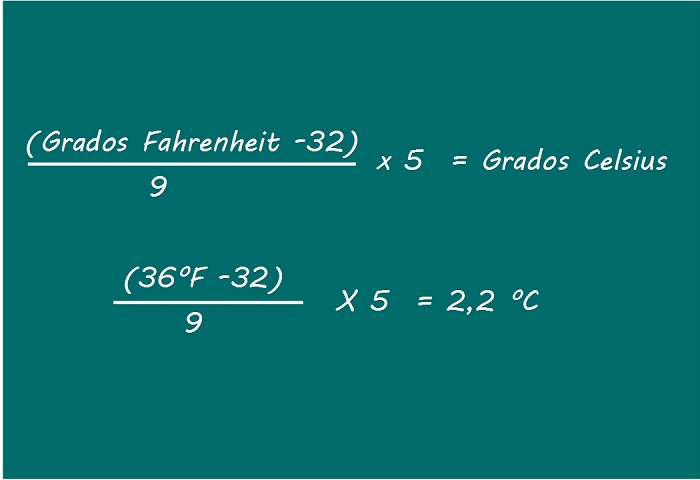
—¿2,2 grados? ¡Qué frío, Mati! —dijo Ven acurrucándose junto a la pelirroja.

—Sí, bastante frío, la verdad. Y, ¿sabéis qué? Cuando Fahrenheit diseñó su escala, se midió su temperatura corporal y tenía 100ºF, ¿qué os parece?

Sal y Ven se pusieron a hacer sus cuentas en la pizarra de Mati y concluyeron:

—37,777ºC, Mati —dijo el gafotas.

—Casi malito…—añadió Ven con cara tristona —Mamá dice que con 38ºC ya estamos malitos…

—Sí, efectivamente, estaba un poco destemplado, pero no le pasó, nada, Ven, no te preocupes —tranquilizó al pequeño —Pues, ¿sabéis qué?, además de estas dos escalas, la Celsius y la Fahrenheit, existe otra escala, la de Kelvin, que es la que usan principalmente en investigación, que se representan con K, sin cerito, y que no se llaman grados, por ejemplo 36 K, se dice 36 kelvins y son -237,15 ºC —dijo Mati mientras les guiñaba un ojo —Un poco más de frío, ¿no?

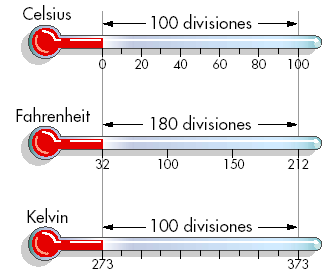
Los dos hermanos la miraban con los ojos redondos como platos y hasta Gauss parecía temblar de frío.

—Bueno, frioleros, ¿veis como 8 no es siempre el doble de 4? ¿Que depende de la escala con que estemos midiendo?

—Bueno, si hablamos de temperaturas…

—O de terremotos —contestó Mati.

—¡¿Cómo?! —Ven tenía ahora frío y miedo —no me gustan los terremotos.

—Ni a ti ni nadie, creo, cielo. Pero con los terremotos pasa lo mismo, un terremoto de magnitud 8 (en la escala Richter) no es el doble de un terremoto de magnitud 4 en la misma escala, sino que es 10000 veces más grande.

—¡Toma, toma, toma! —dijo el pequeño mientras desencajaba la mandíbula y el gafotas desviaba la mirada hacia algún punto en su mente.

—¿Por qué? —terminó preguntando Sal.

—Pues porque la escala Richter es una escala logarítmica, en base 10, y cada grado que sube es como si multiplicáramos por 10. Un terremoto de grado 5, es 10 veces mayor que uno de grado 4, uno de grado 6 es 100 veces mayor que el de 4, uno de grado 7, 1000 veces y el de grado 8 será 10000 veces mayor.

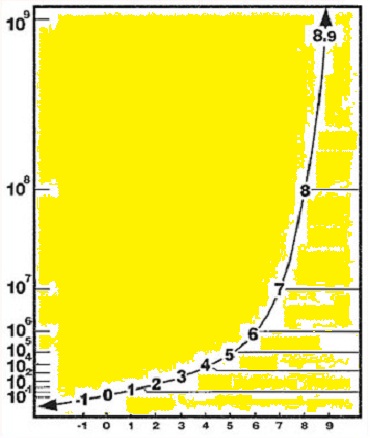
—¡Qué complicado, Mati! —protestó Ven —¿por qué lo hacen así?

—Bueno, Ven, en general, las escalas logarítmicas son muy útiles cuando los valores que vamos a tomar pueden variar mucho y se usan mucho en procedimientos científicos. De hecho, la escala Richter sólo se usa en California, fuera de allí se llama escala de magnitud del momento. O sea, que la magnitud de los terremotos de la isla de El Hierro, se están midiendo con esta última escala, que es también un escala logarítmica como la de Richter.

—Bueno, creo que me voy al jardín. Sí, no hace tanto frío, nada de frío… —dijo Ven tomando en brazos a Gauss y saliendo del salón.

Mati y Sal se miraron, sonrieron, entendieron el mensaje y salieron tras él.

Pues sí, hay distintas escalas para medir la temperatura, y las tres más conocidas son la de Celsius, la de Fahrenheit y la de Kelvin.

Y en cuanto a terremotos, la más conocida es la escala de Richter, aunque los sismólogos no utilizan esa escala, sino la escala sismológica de magnitud del momento. De hecho, la de Richter sólo se usa en la falla de San Andrés, en California, con la medida realizada por un sismógrafo en particular y tiene un valor máximo en 6,8. Al modificarla para medir magnitud local en otras zonas, dejó de llamarse así. Sin embargo, la gente la conoce como escala de Richter porque los periodistas se empeñan en añadir ‘de Richter’ cuando se habla de magnitud local. Lo tenéis muy bien explicado en esta entrada de Microsiervos.

En este episodio de nuestras Mateaventuras, además de informar sobre estas escalas, lo que pretendíamos es llamar un poco la atención sobre otras afirmaciones que también leemos a veces en la prensa, por ejemplo, que nos ‘explican’ que un terremoto de intensidad 9 es el doble de intenso de uno de 4,5 y esas cosas, cuando no es así.

Y parafraseando un dicho español popular “Nada es verdad ni mentira, todo depende de la escala con que se mida”.