Al norte del paralelo 38

—¡Ni hablar, Ven! ¡El abuelo me lo dio a mí!

—Pero ¿qué dijo, Sal? ¿Eh? ¿Qué dijo? —protestó Ven y añadió tratando de imitar a su abuelo Alberto —”Os regalo este sombrero” ¡A los dos!

—Ya, Ven —dijo el gafotas —, pero lo he cogido yo antes. Se siente…

—El que lo vas a sentir eres tú —gruñó el pequeño —, te dije que este año yo iba de buscador de oro del Klondike.

—¿¿En Canadá?? —preguntó Sal extrañado —¿¿Con un salacot??

—¡Sí! ¿Qué pasa? —se enfrentó Ven con determinación.

—Que te vas a morir de frío en Canadá con un salacot… —dejó caer Sal.

—Pero ¡si vamos a Cádiz!

—Ya, pero ningún buscador de oro de Dawson City llevaría un salacot —añadió Sal —, me queda mejor a mí para ir a buscar las fuentes del Nilo...

—Pero bueno —Mati acababa de llegar —, que carnaval tan aventurero… Desde Canadá hasta Tanzania…

—Hola, Mati —la saludó Sal.

—Hola —dijo Ven —. Sal es un abusón y se quiere quedar con el salacot que nos ha regalado el abuelo Alberto y ¡yo lo quiero para mi disfraz de buscador de oro!

—Hola, chicos —dijo ella —. Lo cierto es que Sal tiene un poco de razón, un salacot es más apropiado para climas cálidos… Por otra parte, esa región de Canadá tan cerca de Alaska es un poco peligrosa para ti —Mati le guiñó un ojo a Ven —, está llena de osos.

—No pasa nada, Mati —respondió Ven con entereza —, sé perfectamente cómo actuar ante cualquier oso: polar, negro o pardo.

—¿Ah, sí? —preguntó la pelirroja muy interesada.

—Sí —contestó él impasible —. Si es pardo, me acurruco como un bebé, si es negro le tiro piedras y lo insulto y si es polar…

—Si es polar no hay nada que hacer, Ven —añadió Sal —, no puedes escapar de un bicho que corre a 40 kilómetros por hora sobre placas de hielo…

—Vaya —intervino Mati —, os veo muy informados sobre osos.

—Nos lo leyó mamá de un libro de Javier Reverte —dijo Sal —, El río de la luz.

—Ajá, ya veo —respondió ella —. Y tu búsqueda de las fuentes del Nilo, ¿también está relacionada con un libro de Reverte?

—¡Sí! —exclamó el gafotas —¿Cómo lo sabes?

—Digamos que a mí también me gustan mucho sus libros —dijo Mati —¿Os apetece que os cuente un acertijo sobre exploradores y osos?

—¡Vale! —dijo Sal inmediatamente.

—Bueno, venga —aceptó el pequeño que no se fiaba mucho de su hermano.

—Un explorador sale una madrugada de su tienda, anda 10 Km al Sur, después 10 Km al Este, por último, 10 Km al Norte y llega de nuevo a su tienda. Dentro de su tienda, encuentra un oso. Pregunta —Mati hizo una pausa dramática —: ¿De qué color es el oso?

—¿¿Quééééééééé?? —preguntó Ven con la cara arrugada.

—Estás de broma, ¿no, Mati? —agregó Sal.

—No, no lo estoy —respondió esta — ¿Sabéis de que color era el oso o no?

—Y yo que sé… —aceptó tímidamente Ven.

—Pero si es muy fácil —se burló un poco Mati —¿Os rendís?

Los niños asintieron con la cabeza, Gauss hizo como que no había oído el acertijo.

—El oso era blanco —anunció la pelirroja.

—¿¿Cómo la sabes?? —preguntó Ven.

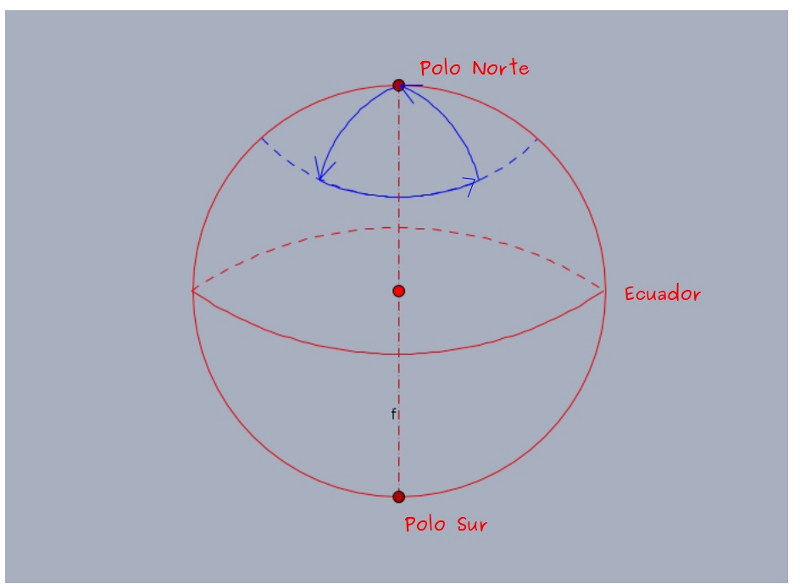
—Pues porque si el explorador caminó 10 Km al sur, 10 al este, 10 al norte y llegó de nuevo a su tienda —les contó —, es porque estaba en el Polo Norte y allí, los osos son blancos.

—Hala, es verdad —comentó Sal muy divetido —, no se me había ocurrido.

—¡Toma, toma, toma! ¡Cómo mola! —exclamó Ven —Se lo voy a contar a todos mis amigos.

—¿Estáis seguros de que el oso era blanco? —preguntó Mati con voz de inspector de policía.

—¡Pues, claro! —afirmó el pequeño con rotundidad.

—Nos lo has dicho tú, Mati —añadió Sal titubeando.

—¿Estáis seguros de que eso solo puede ocurrir en el Polo Norte? —siguió indagando Mati Lestrade.

—¿Qué quieres decir, Mati? —preguntó el gafotas.

—Os pregunto —dijo ella —si es el Polo Norte el único punto de la Tierra en el que si caminas 10 Km al sur, después 10 Km al este y, por último, 10 Km al norte, vuelves al punto de partida.

Los niños se quedaron pensando un rato hasta que, finalmente, Ven exclamó:

—¡Y en el Polo Sur!

—Si estás en el Polo Sur, Ven —le respondió su hermano —no puedes caminar hacia el sur…

Ven hizo una mueca graciosa encogiendo toda su carita al descubrir su pifia, Gauss miró a otro lado.

—Efectivamente, Sal —dijo Mati —, si estamos en el Polo Sur no podemos caminar hacia el sur. Pero, el Polo Norte no es el único punto de la Tierra en el que se puede caminar 10 Km al Sur, luego 10 Km al Este y, por último, 10 Km al Norte y volver al sitio de partida…

—¡Anda que no! —interrumpió Ven súbitamente.

—Pues no, no es el único —le corrigió Mati con un guiño —. De hecho, hay infinitos puntos sobre la Tierra en los que esto ocurre.

—Pero, ¡vamos a ver! —protestó el incrédulo Ven —¡Eso es imposible!

—No, no lo es —dijo Mati con voz de misterio.

—Ven, deja a Mati que nos lo cuente —le pidió su hermano que estaba cada vez má intrigado.

—Os lo contaré —empezó a decir Mati. Sabemos que la longitud de la circunferencia en el Ecuador es, aproximadamente, de 40000 kilómetros, ¿no?

—Sí, nos lo contaste cuando nos hablaste de Erastótenes —puntualizó el gafotas.

—Pues bien —continuó ella —, nos vamos a fijar en un paralelo del hemisferio Sur, uno de las círculos paralelos al Ecuador por debajo de este, que mida de longitud de circunferencia 10 kilómetros.

—Que pequeñito… —masculló Ven.

—Sí, muy pequeño —añadió ella —, será un paralelo muy cercano al Polo Sur. Si ahora buscamos otro paralelo 10 kilómetros al norte del que acabamos de elegir, ya está.

—¿Cómo que ya está? —preguntó Sal.

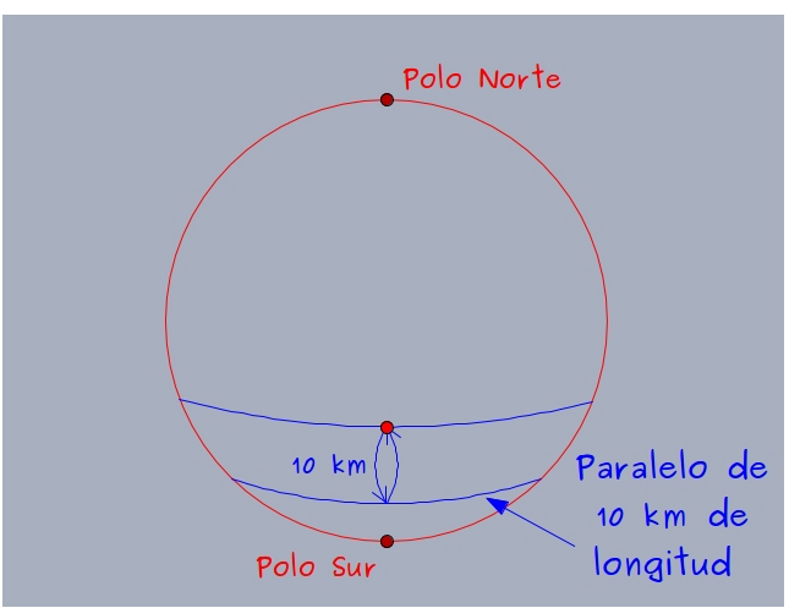
—Sí, fijaos —continuó la pelirroja —. Desde este nuevo paralelo caminamos 10 kilómetros hacia el Sur, nos encontramos con el paralelo que mide 10 kilómetros de longitud, al caminar sobre él 10 kilómetros, volveremos al punto de partida en ese paralelo, y al caminar 10 kilómetros en dirección norte, volvemos al principio.

—¡TOMA, TOMA, TOMA! —gritó Ven entusiasmado.

—Claro… —dijo el gafotas felizmente sorprendido — Y como hay infinitos puntos sobre un paralelo, podemos salir de infinitos sitios diferentes desde el paralelo al norte del paralelo de 10 kilómetros… Maravilloso.

—No se vayan todavía, aún hay más —dijo Mati con voz de falsete —. Si tomamos en lugar de un paralelo de longitud 10 kilómetros, un paralelo de longitud 5 kilómetros y partimos de un punto 10 kilómetros al norte del mismo, ¿qué ocurrirá?

Los niños se quedaron un rato pensando, al cabo del cual Sal dijo:

—¡Que volvemos al punto de partida!

—¿Cómo? —preguntó Ven.

—Bajamos 10 Km al sur, al llegar al paralelo de 5 kilómetros de longitud —explicaba Sal con alegría —, si recorremos 10 kilómetros al Este, habremos dado 2 vueltas al paralelo y volvemos al punto de ese paralelo en el que comenzamos.

—¡MOOOOOOOOOOOLA! —se alegró el pequeño.

—¿Y si nos ponemos 10 kilómetros al norte de un paralelo de longitud 10/3 kilómetros? —preguntó Mati a sus muchachos.

—¡Pues también! —gritó Sal —En ese caso, tendríamos que dar 3 vueltas para recorrer 10 kilómetros y volver al principio.

—Bueno, bueno —intervino Ven —Entonces también vale con un paralelo que mida 10/4 kilómetros. Basta con dar 4 vueltas, ¿no?

—Efectivamente, Ven —dijo Mati —. Y con el de 2 kilómetros de longitud, que sería el correspondiente a 10/5. En general, con cualquier paralelo que mida 10 dividido entre un número natural. Solo tendríamos que situarnos 10 kilómetros al norte de dicho paralelo y al bajar desde allí dar tantas vueltas como nos indique el número natural.

—Fascinante… —suspiró Sal.

—Sí, fascinante —corroboró su hermano.

—Me alegro de que os guste —dijo Mati haciendo una graciosa reverencia.

—Y claro —continuó el gafotas —, esto mismo se podría hacer buscando paralelos de longitud 10 kilómetros y tal alrededor del Polo Norte.

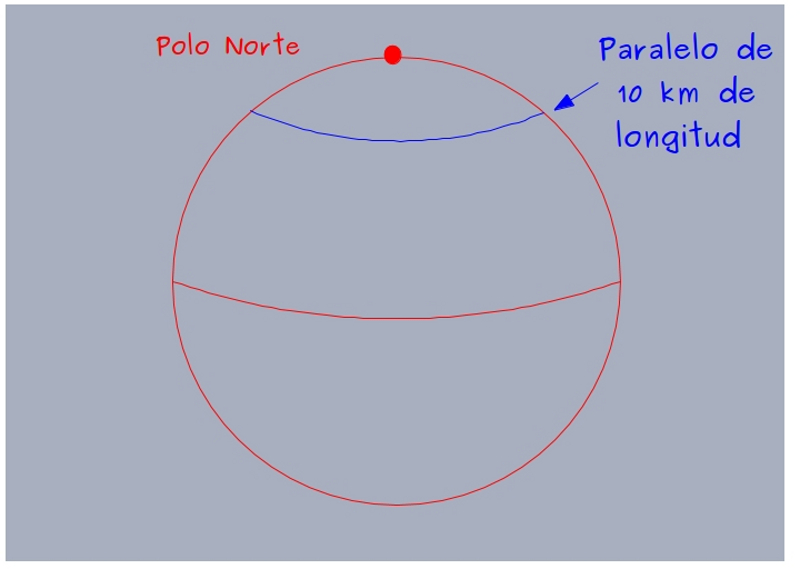
—No —contestó la gafotas con energía —. El paralelo de longitud 10 Km en el hemisferio norte está a menos de 2 Km del Polo Norte, no hay forma de situarse 10 Km al norte sobre él.

—¿Tan cerca? —se extrañó Sal.

—Sí —dijo Mati —. Es un paralelo muy, muy pequeñito…

—Y muy mono… —dijo Ven haciendo carantoñas a su hermano.

—Ven —protestó el gafotas —no seas tan

FIN

Vaya, parece que nuestros protagonistas han desaparecido corriendo de escena, ¿conseguirán correr a más de 40 km/h por el Pequeño Libro de Notas? ;-)

Sólo una cosa, en todo esta mateaventura hemos supuesto que la Tierra es una esfera.

Y nada más, solo recordaros que, digan lo que os digan, nuestro bello planeta, aunque maravilloso, no es el centro del Universo. Lo anterior no impide que amemos y respetemos a este puntito azul pálido.

Traducción y subtítulos por Arturo Quirantes