Más de 37 grados de temperatura...

—Me contó maneras de llegar a la verdad de cualquier tema, no sólo sentándote a pensar en ello como Aristóteles (un señor griego, listo pero confundido), sino saliendo a mirar con tus propios ojos; me habló de hacer hipótesis e idear experimentos, y de comprobar las cosas mediante la observación y llegar a una conclusión… —Sal leía despacio y con pasión aquel párrafo del libro, era uno de sus favoritos.

—Déjalo, Sal —interrumpió Ven con tristeza —. Tengo más de 37 y me duele la cabeza… Además, me da rabia perderme el entrenamiento por este maldito virus…

—No estés triste, Ven —le pidió su hermano —. La semana que viene estarás bien y podrás ir a entrenar.

—Pero yo quería ir hoy… —no había consuelo para el pequeño.

—Bueno, pero no puedes —continuó el gafotas paciente —, y así además, puedo leer para ti como mamá me lee cuando estoy malito.

—Gracias, gafotas, eres el mejor hermano del mundo —dijo Ven más triste que nadie por no poder ir al entrenamiento de fútbol.

—Los dos sois unos hermanos preciosos —dijo Mati que entraba en ese momento por la puerta y dirigiéndose a la mascota añadió —. Tú también eres precioso, Gauss.

—¡Hola, Mati! —la saludó Sal.

—Hola, Mati —dijo Ven con voz de ultratumba.

—¡Oh, Calpurnia Tate! —exclamó Mati —Adoro ese libro…

—Yo también —dijo el gafotas —. Nos lo regaló Fis y me lo lei este verano. Estoy seguro de que Ven se animará un poco con la historia…

—La historia sí que me gusta —interrumpió el pequeño pesadamente —, pero tengo más de 37 y casi no puedo escuchar…

—Vaya, sí que estás malito… —dijo la pelirroja —. Es una pena porque cuando me enteré de que estabas en cama me acordé de un juego que nos gusta mucho a los matemáticos y os lo traje para jugar. Pero, bueno, quizás otro día…

—¿Qué juego es, Mati? —preguntó Ven con un hilillo de voz — ¿Se puede jugar en la cama?

—Claro, cielo —contestó ella —. Se juega sobre un tablero, o sobre un papel si no tenemos un tablero.

—Yo creo que puedo hacer un esfuerzo, Mati —dijo Ven un poco dramático.

—¿Qué juego es, Mati? —preguntó Sal ansioso — ¿Sudoku?

—No, no —dijo esta —. Es un juego que puede recordar, en algún sentido al tres en raya o al Quarto.

—¿Hay que construir líneas con las fichas? —siguió indagando el gafotas.

—No, exactamente —respondió Mati con misterio —. Se trata de hacer caminos, pero no tienen por qué ser en línea recta…

—¿Nos lo enseñas, Mati? —dijo Ven incorporándose de súbito en la cama.

—Claro, claro —dijo ella —. Pero no te sulfures, que te subirá la fiebre.

—Es verdad, Ven —corroboró Sal —. Te conviene descansar…

Ven volvió a tumbarse sobre sus almohadones con cara de más malito que nadie.

—Bueno, ¿están listos estos dos caballeros? —preguntó Mati con voz teatral —. Es un honor para mí presentarles, tachán, tachán, ¡el Hex!

—¿Cómo has dicho? —preguntó Ven.

—Hex —contestó ella —Se llama así porque las casillas del tablero son hexágonos. Os he traído un tablero y fichas, pero se puede jugar con papel. Sólo hay que dibujar un rombo usando hexágonos, como por ejemplo este:

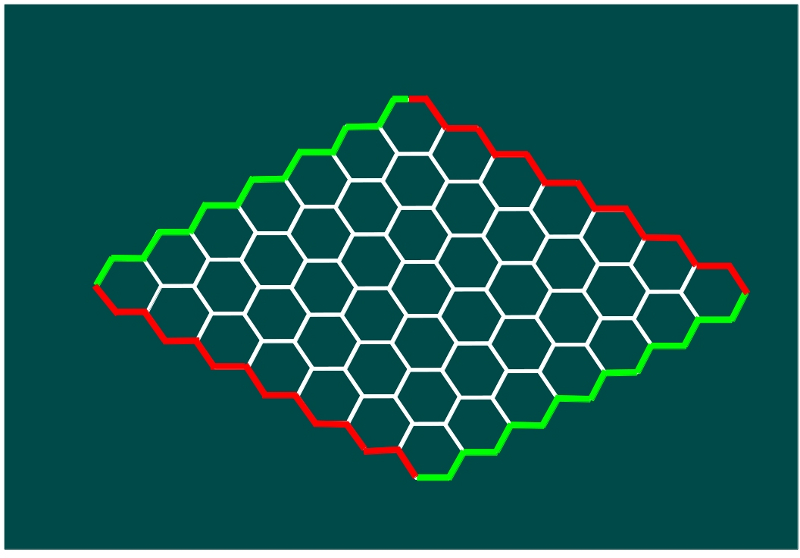
—¿Veis? —continuó Mati —Este es un tablero 7 por 7, lo usual es jugar en un tablero, al menos, 10 por 10. Hemos pintado dos lados de rojo y otros dos de verde. Ahora, cada uno de vosotros tendrá 25 fichas, verdes para Sal , por ejemplo, y rojas para Ven. Por turnos, los jugadores, van poniendo sus fichas en el tablero, sin ninguna restricción, y gana el que consiga un camino que una los dos lados de su color correspondiente. Mirad, en la partida que aparece en la siguiente figura, habrían ganado las fichas verdes.

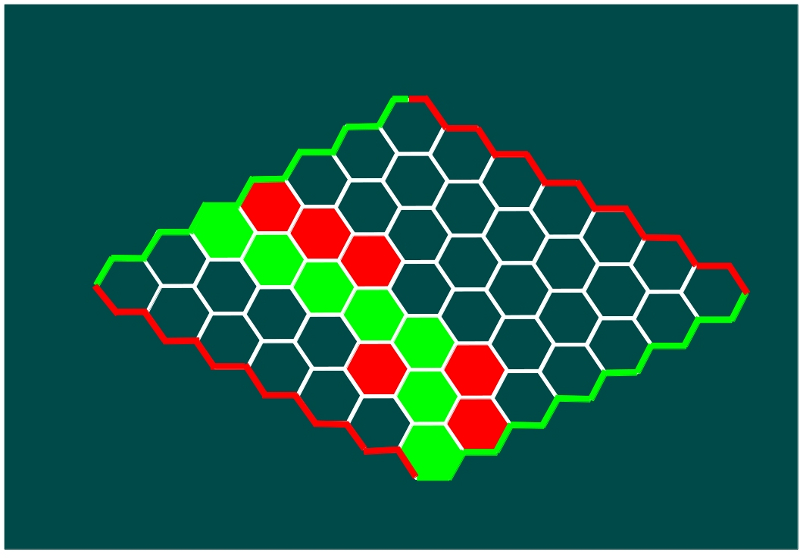
—Claro, ha tenido que ganar Sal —se quejó mimoso el pequeño.

—Pero si es un ejemplo, Ven —añadió sal con ternura — ¿Y si ninguno de los jugadores consigue hacer el camino porque el otro se lo impide todo el rato?

—Empatan, claro —apostilló Ven.

—No, es imposible empatar —anunció Mati —¿Os acordáis del Algoritmo del matrimonio estable que os conté cuando ibáis a la nieve?

—¡Sí! —exclamó Sal — El que consiguió el Nobel de Economía en 2012, ¿no?

—El mismo —corroboró Mati —. El Nobel se lo concedieron a Al Roth y Lloyd Shapley, por aplicar el algoritmo en Economía, pero el diseño del algoritmo fue de Lloyd Shapley y David Gale…

—¡Qué morro! —se quejó Ven —¿Por qué no le dieron el Nobel también a David Gale?

—Porque el señor Gale murió en 2008, Ven —le dijo Mati —. El premio Nobel solo se concede a gente viva.

—Pobre… —la barbilla de Ven comenzó a temblar.

—Pues bien —continuó la pelirroja tratando de desviar el tema —, David Gale demostró, en 1979, que es imposible el empate en el Hex y que este hecho implicaba el teorema del punto fijo de Brouwer, pero esto último es muy complicado aún para vosotros.

—¿Seguro, seguro que no hay empate? —preguntó Sal desconfiado.

—Seguro —confirmó Mati —. Si llenas el tablero de fichas rojas y verdes, de la forma que quieras, siempre tiene que haber o un camino rojo conectando los lados rojos, o un camino verde conectando los lados verdes.

—No sé, no sé… —Sal no parecía muy convencido.

—Se puede demostrar usando Teoría de Grafos —continuó Mati —pero creo que es mejor que juguemos, ¿no?

—¡Sí! —exclamó Ven — yo te creo, Mati.

—Es más —añadió ella —Os voy a enseñar unas estrategias para que ganéis siempre que juguéis al Hex; siempre que juguéis con un tablero 4 × 4 o en un tablero 5 × 5 y seáis el primero en empezar.

—¡Mola! —dijo Ven.

—Allá vamos —anunció Mati —. Dibujamos un tablero 4 × 4, así:

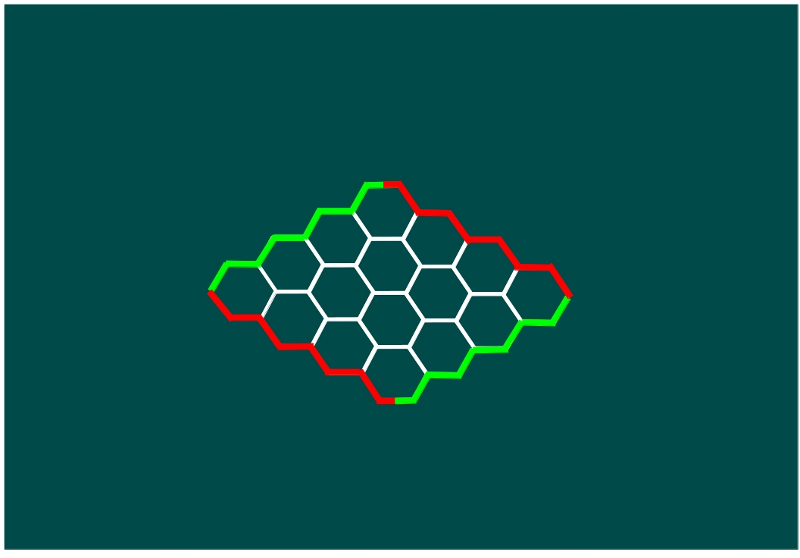
—Pues bien —continuó ella —, si el primer jugador, que será Ven, porque está malito, coloca su primera ficha en la siguiente posición, ya ha ganado.

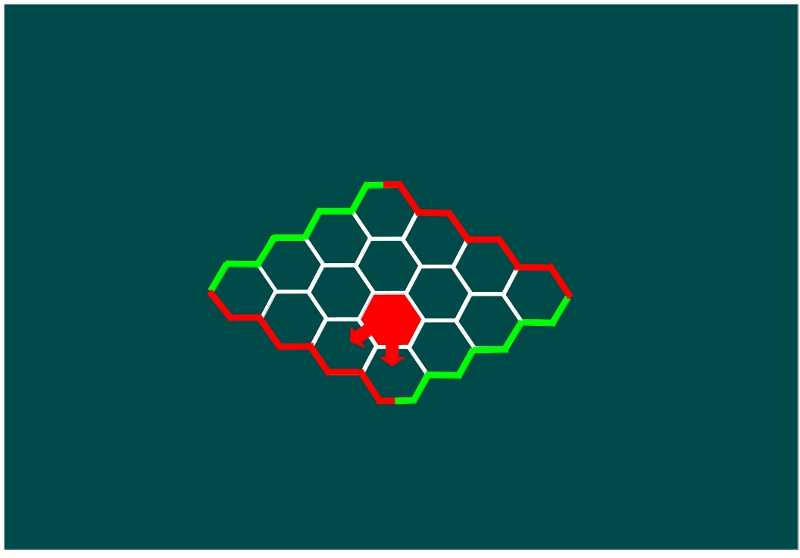
—Sí, claro —dijo el pequeño desconfiado.

—¿Cómo lo sabes, Mati? —preguntó Sal.

—Fijaos en las dos flechas que señalan dos hexágonos vecinos —les dijo —. Si Ven coloca su segunda ficha roja en uno de ellos, ya habrá llegado a una de las orillas rojas del tablero, ¿no?

Los niños asintieron con la cabeza. Gauss bostezó.

—Pero Sal, con sus fichas verdes —siguió —, solo puede ocupar una de ellas, con lo cual, con su segunda ficha roja, Ven ha llegado a la orilla, por ejemplo, como aquí:

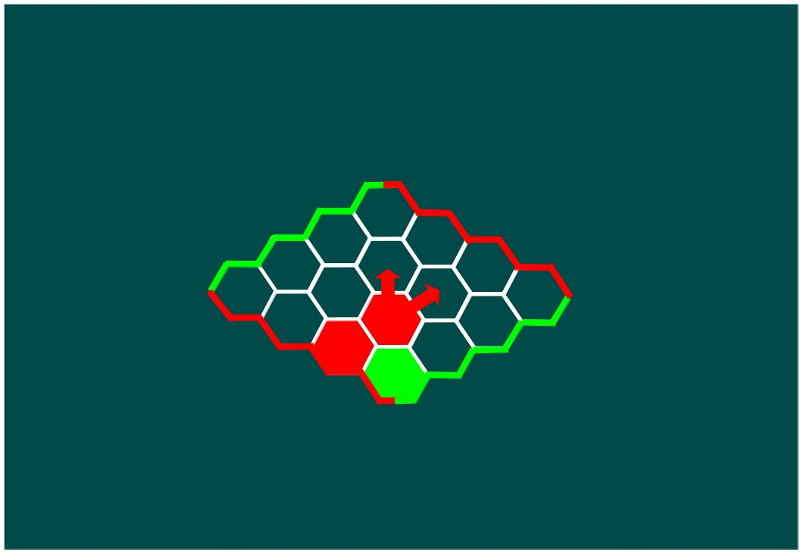
—Vamos a continuar el camino rojo hacía la otra orilla —propuso la gafotas —, en alguna de las dos direcciones que señalan las fechas. Sal solo puede bloquear una de ellas con su próxima ficha verde, ¿no?

Los niños volvieron a asentir. Gauss se rascó la cabeza.

—Ahora fijaos en la siguiente pizarra —les dijo —Ponga donde ponga Sal la siguiente ficha verde, colocando la ficha roja en la otra opción, llegamos a una celda que tiene dos opciones para llegar a la orilla.

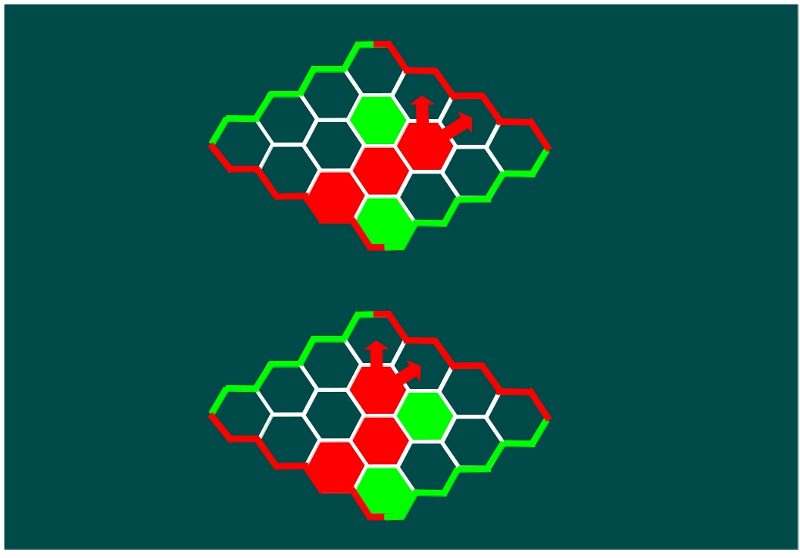
—Ya ha ganado Ven —aseguró Mati.

—¡Toma, toma, toma! ¡Cómo mola! —gritó Ven.

—Pero, ¿tú no estás malito? —preguntó Sal a su hermano mirándolo por encima de las gafotas.

Ven tosió y frunció el ceño con cara de dolor.

—Claro —observó Sal —, en cualquiera de esas dos posiciones, haga lo que haga la verde, ya ha llegado… Me gusta ¿Nos cuentas cómo ganar en el tablero de 5 × 5?

—Con mucho gusto —respondió Mati con una reverencia —.Para que Ven gane en el Hex de tamaño 5 por 5, es suficiente que las rojas comiencen en esta posición:

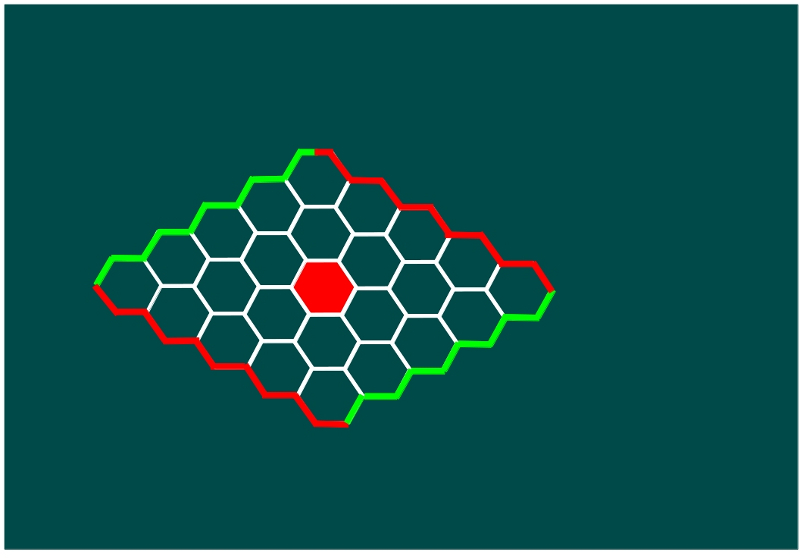
—Para construir el camino rojo hacia la orilla roja superior —les contó Mati —elegimos la celda superior a la roja elegida, o la que está a la derecha de esta. Una de las dos, al menos, estará libre después de que jueguen las verdes. Suponemos que la verde se coloca justo por encima, cogemos la otra y ya llegamos a la orilla en la siguiente jugada.

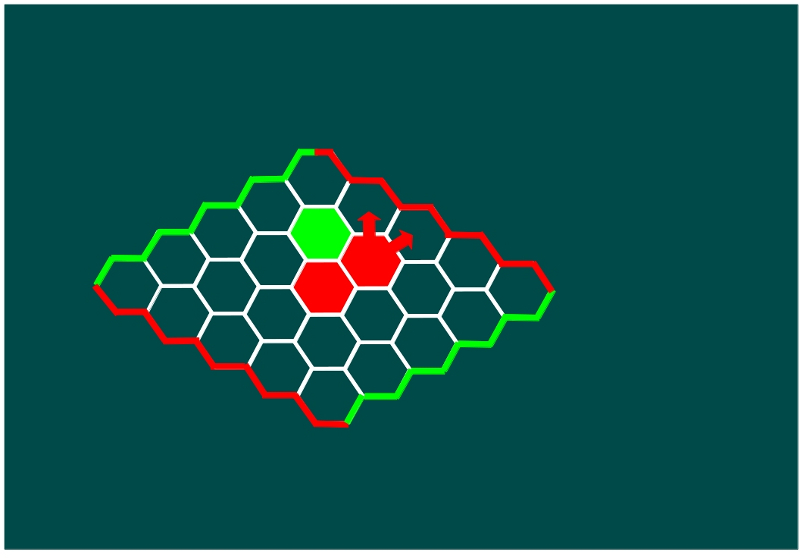
—¡¡Mola!! —gritó Ven y rápidamente puso de nuevo cara de malito.

—Ahora, vamos a construir el camino hacia la orilla roja inferior —siguió ella —, bien en la celda de abajo de la primera que elegimos, bien la que está a la izquierda de esta, una de las dos tiene que estar libre después de que jueguen las verdes. Supongamos que Sal nos bloquea con una ficha verde en la celda de abajo, nos ponemos en la celda a su izquierda

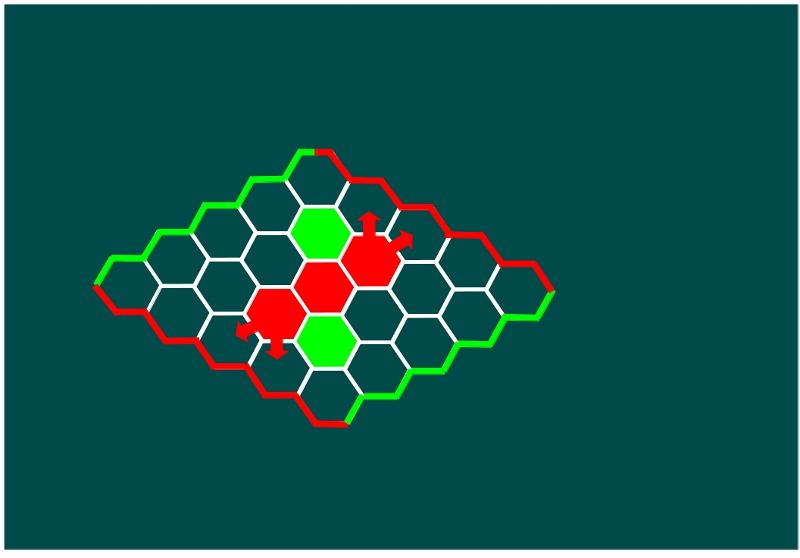
—¡Toma, toma, toma! —empezó gritando Ven y terminó con voz de penita —He vuelto a ganar.

—Mola… —dijo Sal.

—Si las rojas empiezan en esa posición —concluyó Mati —aquí tenéis todas los posibles caminos para ganar a las verdes, en función de los movimientos que hagan estas.

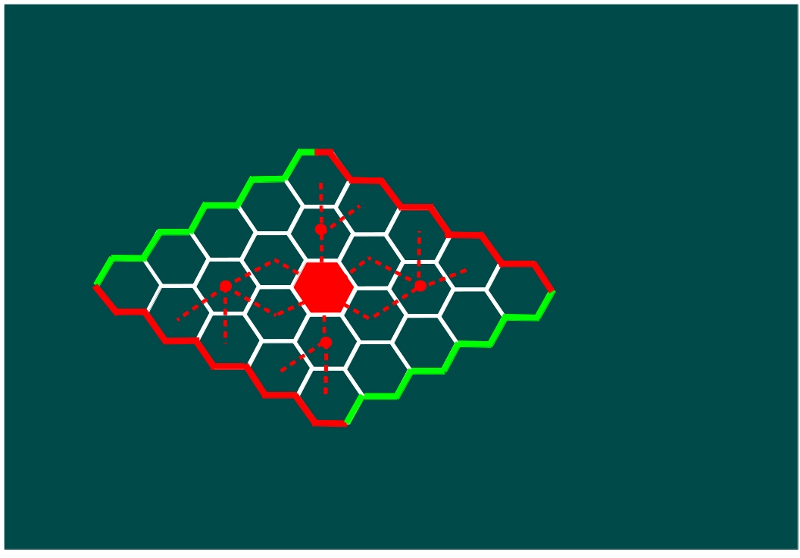
—¡Toma, toma. toma! ¡Cómo mola! —volvió a exclamar Ven.

Sal lo miró de reojo y preguntó:

—¿Hay un método para ganar en cualquier tablero de cualquier tamaño, Mati?

—Me alegro de queme hagas esa pregunta —dijo esta muy teatrera —. Está probado que siempre existe una estrategia ganadora, pero solo se conocen, hasta donde yo sé, para tableros de hasta 9 por 9.

—No entiendo —se extrañó el gafotas —, si solo se conocen hasta 9 por 9, ¿cómo sabes que siempre se puede?

—Pues, ya verás —respondió Mati —, porque otro matemático con premio Nobel de Economía, John Nash, demostró que siempre había estrategia ganadora. Pero la demostración del señor Nash no era constructiva, es decir, no describía la estrategia, solo que existía la misma.

—Además —continuó contándoles Mati —, John Nash es conocido como el inventor del Hex, junto con otro matemático danés, Piet Hein, porque lo descubrieron independientemente. De hecho, cuando John Nash inventó el juego, en la Universidad de Princeton a este juego se le llamaba “Nash” e incluso, “John” en su honor. Nash buscaba el juego perfecto para los matemáticos, cuentan que él creía que era el HEX de 14 por 14.

—Qué tío —dijo Ven —, debía ser muy listo.

—Sí, lo es, aún vive —continuó Mati —. Muy listo y bastante especial. Aparte de por sus trabajos, Nash es muy conocido a nivel mundial a partir de un libro que sobre él escribió Sylvia Nasar y que fue adaptado posteriormente a una película:“Una mente maravillosa”.

—¿Por qué dices que es especial, Mati? —quiso saber Sal.

—Digamos que es un poco excéntrico —dijo esta —, en la película aparece, por ejemplo, garabateando fórmulas matemáticas por las paredes, puestas, ventanas…

—Qué loco… —dijo Ven sonriendo y, posiblemente, perpetrando imitar al señor Nash cuando de recuperara.

—Mati —preguntó Sal de repente —, ¿tú crees que el Hex 14 × 14 es el juego perfecto para los matemáticos?

—Bueno, —respondió esta —,entre los matemáticos, como en cualquier grupo humano que elijamos, hay personas muy, muy diferentes y con gustos muy distintos. Me gusta mucho jugar al Hex, pero sigo opinando que me gusta más el Quarto.

—¡Y a mí! —exclamó el enfermito.

—Otra cosa que no entiendo, Mati —preguntó Sal —, estos matemáticos, Shapley y Nash, ¿tienen premio Nobel de Economía? ¿Por qué no de Matemáticas?

—Porque no existe el premio Nobel de Matemáticas, entre otras cosas —respondió ella.

—¿¿Por qué?? —preguntó Sal.

— Hay muchas teorías —le respondió ella —, pero aquí, entre vosotros y yo, yo creo que, básicamente, porque al señor Nobel no le gustaban las matemáticas.

—¡Fijaos! —gritó Ven de repente —¡Parece que tenemos otro futuro premio Nobel de Economía en casa!

FIN