Habitación 35

—¿Seguro que es la 35, Sal?

—Seguro, Ven, confía en mí.

—Es que hay tantas puertas… —dijo Ven —Éste sí que parece el hotel de los líos…

—Qué exagerado eres, Ven, todos los hoteles tienen un montón de puertas.

—¿Habéis encontrado nuestra habitación? —preguntó Mati que se unía al grupo de turistas.

—Sí, aquí está, la 35 —respondió el gafotas.

—Hay tantas puertas que me mareo… —añadió Ven muy teatrero, Sal resopló con cansancio.

—Me has recordado un acertijo que tiene que ver con puertas de un hotel —anunció Mati —Si queréis os lo cuento.

—¡Sí! —dijeron los hermanos al unísono, Gauss gruñó porque sabía que durante un rato nadie le haría caso.

—Érase una vez un botones de un hotel que se volvió un poco majareta —empezó a contarles Mati —Una mañana se fue a un pasillo del hotel, en el que había 10 puertas, numeradas del 1 al 10, y las abrió todas.

—¡Qué loco! —dijo Ven sonriendo.

—Calla, Ven —le pidió su hermano.

—Cuanto tuvo las 10 puertas abiertas —continuó la pelirroja —decidió cerrar todas la habitaciones que tenían un número par.

—¿Por qué? —preguntó el pequeño.

—Porque estaba majareta —respondió ella —Después, se fijó en las puertas cuyos números eran múltiplos de 3 y cerró las que estaban abiertas y abrió las que estaban cerradas.

— Es decir —mascullaba el gafotas —Cerró la 3 que estaba abierta, abrió la 6 que estaba cerrada porque es par, y cerró la 9 que estaba abierta.

—Eso es —confirmó ella —Después cambió de estado las puertas de las habitaciones que eran múltiplo de 4, es decir, las que estaban abiertas las cerró y las que estaban cerradas las abrió.

—O sea que abrió la 4 y la 8 que estaban cerradas, ¿no, Mati? —preguntó Ven.

—Efectivamente, cielo —respondió Mati y continuó —Luego hizo lo mismo con las puestas múltiplos de 5, después con las que eran múltiplos de 6, después de 7 y así, hasta que en la última vuelta solo modificó las puertas múltiplos de 10…

—O sea, solo la 10 —intervino Sal.

—Eso es —dijo ella —Ahora viene la pregunta…

—¿Qué le pasaba al botones? —interrumpió Ven con una sonrisa pícara.

—¡Jajajajajajajajajaja! No, Ven —le contestó Mati —La pregunta es ¿qué puertas estarán abiertas al final?

Los niños se quedaron un rato muy serios pensando… Gauss también puso cara de interesante.

—La 1 se queda abierta seguro… —decía Ven —porque el botones solo pasa una vez, la primera.

—La 2 se queda cerrada —añadió Sal —porque cuando pasa la segunda vez la cierra y ya no vuelve a pasar…

—Podemos ir rellenando en una tabla —les propuso Mati —el estado de las puertas después de cada vuelta que daba el botones. Pintamos de verde la puerta que está abierta y de rojo la que esté cerrada. En la primera vuelta, el botones abre todas las puertas

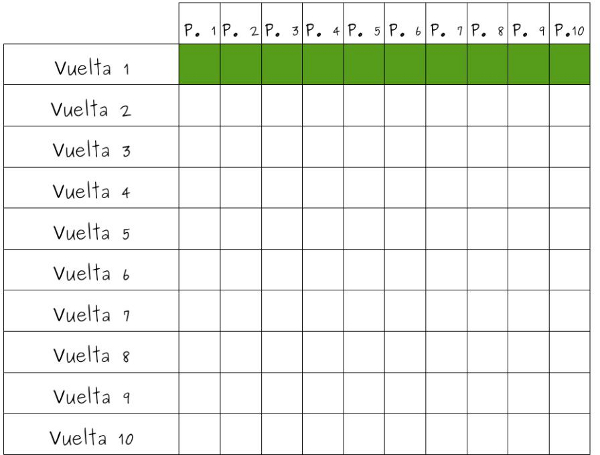
—En la segunda vuelta —continuó la pelirroja —Cierra las puertas pares, o sea, las que son múltiplos de 2.

—Ahora tiene que cerrar las 3 y la 9 —dijo Sal —y abrir la 6, porque son las 3 habitaciones múltiplos de 3.

—Ajá —confirmó ella.

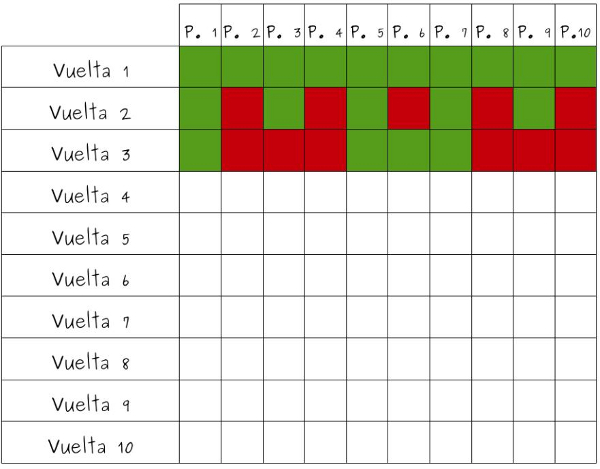
—Y ahora —continuó Ven —es cuando tiene que abrir la 4 y la 8.

—Muy bien, Ven —dijo Mati

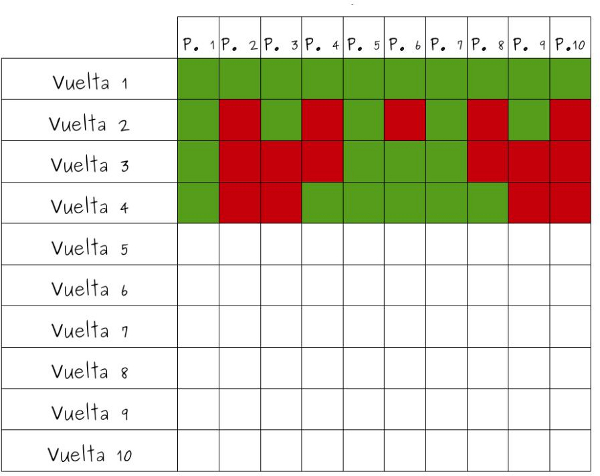
Al cabo de un rato, los niños tenían la tabla completa.

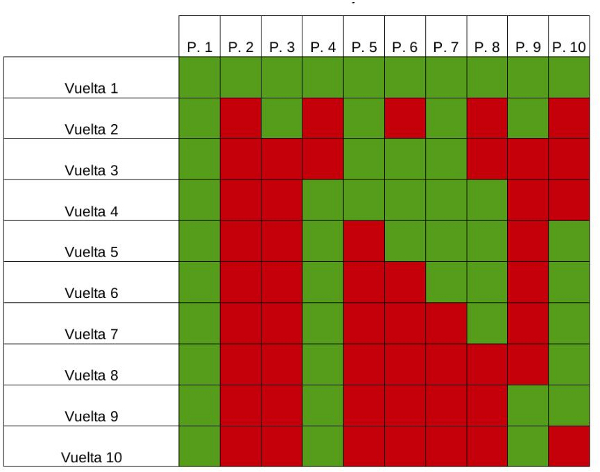
—¡La 1, la 4 y la 9! —gritó Ven de repente —Ésas son las que quedan abiertas.

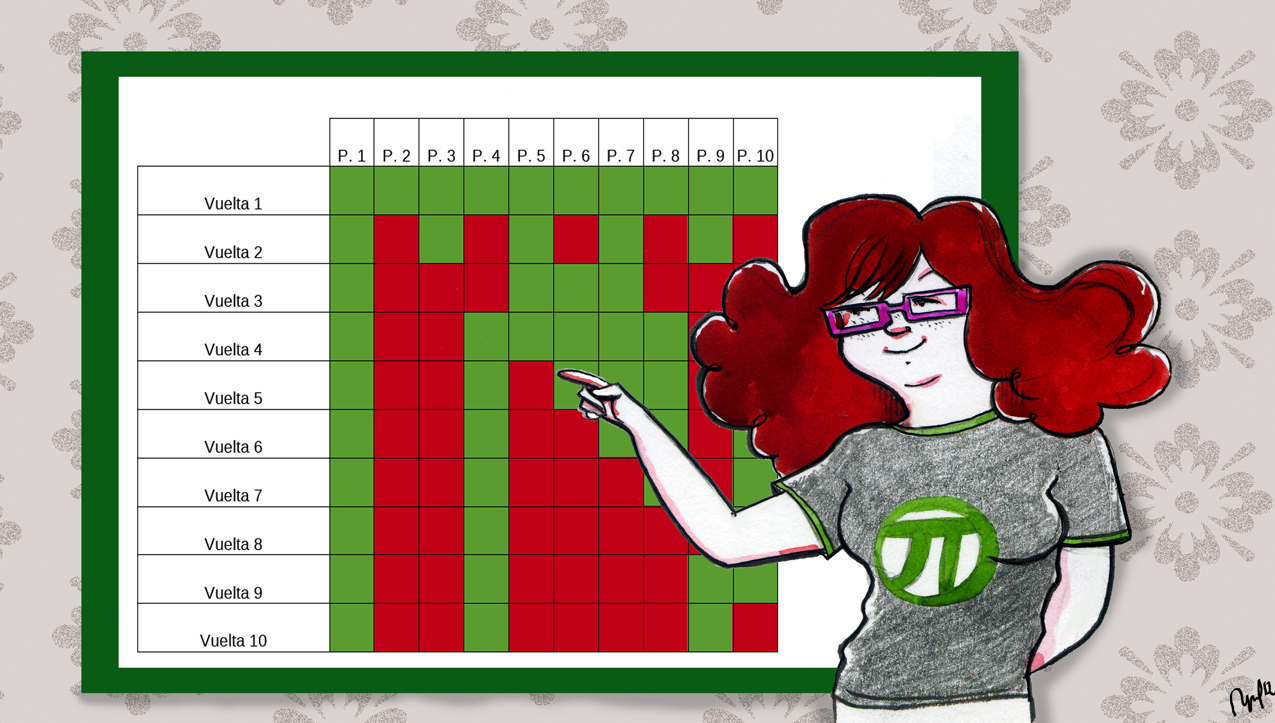
—Efectivamente —dijo Mati —¿Y qué tienen de especial esos 3 números que no tienen los demás?

Otra vez los dos hermanos se quedaron pensativos, Ven miraba de reojo a Sal confiando en que su hermano encontrara la respuesta.

—¿Que son 1, 2 y 3 al cuadrado, Mati? —dijo el gafotas al cabo de un rato.

—Pero, bueno —se sorprendió ésta —¡Eso es! ¡Qué chicos más listos!

—¡Toma, toma, toma! —dijo Ven —¡Mi hermano mola todo!

— Y ¿sabéis qué? —les dijo Mati —si lo hacemos con 100 puertas el resultado es el mismo: las únicas puertas que quedarán abiertas son aquellas cuyo número sea un cuadrado perfecto: 1, 4, 9, 16, 25, 36, 49, 64, 81 y 100.

—¿Por qué, Mati? —preguntó Sal enseguida.

—Vamos a pensar cuántas veces cambia el botones el estado de una puerta —les dijo —Si el número es primo (sus únicos divisores son el 1 y él mismo), por ejemplo el 5, el carcelero solo pasa dos veces. En la vuelta 1 y en la vuelta 5, o sea la abre, y después la cierra.

—¡Toma, claro! —dijo Ven.

—O sea que los números primos quedarán cerrados al final —continuó Mati —El resto de las puertas, serán modificadas tantas veces como divisores tenga. Por ejemplo, el 6 tiene 4 divisores, 1, 2, 3, 6. Como el número de divisores es par, el botones pasará un número par de veces, y se quedará cerrada.

—Claro —pensaba Sal en voz alta —Abierta, cerrada, abierta, cerrada.

—En general —dijo Mati —Si el número de divisores de un número es par, esa puerta estará cerrada al final, ¿verdad?

Los niños asintieron con la cabeza.

—Pues bien —les dijo —solo los cuadrados perfectos tienen un número impar de divisores.

—¿Por qué? —insistió Sal

—Cualquier número natural mayor que 1 se puede expresar como producto de sus factores primos, de forma única, salvo el orden, claro —empezó a contar Mati.

—No entiendo —admitió Ven torciendo la boquita.

—Por ejemplo, si piensas en 18 —dijo ella —se puede escribir como

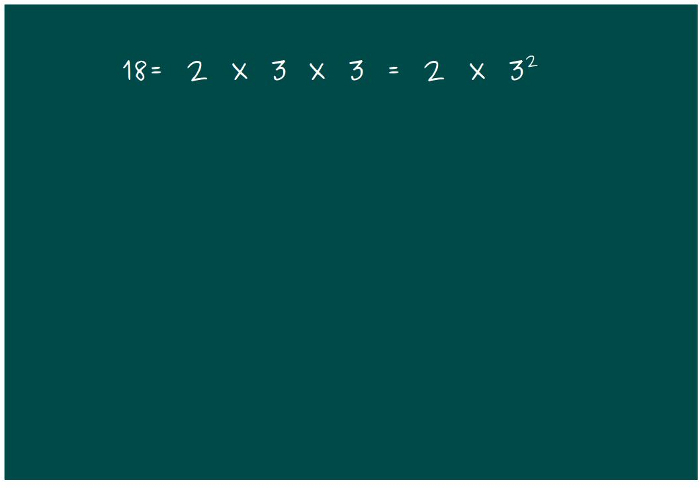
—También se puede escribir como 6 por 3, Mati —dijo Sal.

—Sí, pero 6 no es primo, porque tiene 4 divisores: el 1, el 2, el 3 y el 6 —contestó Mati —Y los números primos solo tienen 2 divisores, el 1 y ellos mismos.

—Entonces, vale —afirmó Ven con cara de interesante —Porque 2 y 3 son bastante primos….

—Ahora vamos a contar cuántos divisores distintos tiene 18 —les propuso la pelirroja.

—1, 2, 3, 6, 9, y 18 —dijo el gafotas.

—Efectivamente, Sal —corroboró ella —que se forman con todos los posibles productos de un número de la lista {1,2} y un número de la lista {1,3, 3²}

—¡Toma! Es verdad… —exclamó el pequeño.

—Por lo tanto —continuó nuestra amiga —sabemos que 18 tiene 6 divisores, el resultado de multiplicar el número de elementos del conjunto {1,2}, esto es, 2, por el número de elementos del conjunto {1,3, 3 ²}, esto es, 3.

—Ajá… —asintió el gafotas esperando impaciente el desenlace de esta historia.

—Pues ahora pensemos en un número cualquiera, le llamamos n, y pensemos que al descomponerlo en producto de factores primos tenemos que n es igual a a ⁱ x b ^j —les dijo —Vamos a contar cuántos divisores distintos tiene n. En un conjunto ponemos {1, a, a ², a ³,…, aⁱ}, que tiene i+1 elementos, y en el otro {1, b, b ², b ³,…, b^j}, que tiene j+1 elementos. Por lo tanto, n tendrá (i+1) x (j+1) divisores.

—Resumiendo un poco para que no nos perdamos —siguió Mati —queremos saber qué puertas quedarán abiertas después de que el botones majareta pase abriendo y cerrando. Sabemos que el botones cambia tantas veces la puerta como divisores tenga el número de la habitación y que se quedará abierta sólo si tiene un número impar de divisores, ¿no?

Los niños asintieron con la cabeza, Mati continuó:

—Ahora sabemos que el número de divisores de un número que se descomponga en factores primos como a ⁱ x b ^j es (i+1) x (j+1). Para que este número sea impar, deben ser impares (i+1) y (j+1).

—Pero si (i+1) y (j+1) son impares —continuó la gafotas —tenemos que tanto i como j son pares, o sea, que i es de la forma 2k y j será de la forma 2m.

—Pues ya lo tenemos, n debe ser el cuadrado de un número, concretamente si i es de la forma 2k y j de la forma 2m, entonces n es igual a a ^2k x b ^2m y por tanto n es el cuadrado de a ^k x b ^m.

—¡Toma, toma, toma! ¡Cómo mola! —gritó Ven.

—Con esto podemos saber el resultado para 1000 puertas —dijo el gafotas —o para 10000, o para 100000…

—¡O para infinitas! —exclamó Ven.

—¿Un hotel con infinitas habitaciones, Ven? —preguntó Sal mirando de reojo a su hermano.

—No creas, Sal —intervino Mati —Otro día os hablaré de un hotel como ése.

—Pero en ese hotel infinito no podremos jugar a esto, ¿no? —dijo Ven divertido —Necesitaríamos un botones demasiado majareta…

FIN

Efectivamente, solo los cuadrados de números naturales tienen un número impar de divisores. En nuestra mateaventura solo lo hemos visto para números de la forma a ⁱ x b ^j, pero, evidentemente, esta misma prueba se puede adaptar para números naturales con cualquier descomposición en números primos.

Hasta muy pronto.

MATI