Dime, D'Hondt, ¿cómo elijo a 32?

—Pero si yo voy a votar a tu curso, Sal, ¡no es justo!

—¡Ven, no se puede obligar a nadie a votar lo que tú quieres! —protestó el gafotas —Eso no es democrático, ¿sabes?

—Ni democrático ni flores, Sal —insistía el pequeño —Si no votas a 3ºA puede que yo me quede sin ir al estadio, ¿sabes?

—Pero iremos el fin de semana con el abuelo, —siguió Sal —nos lo prometió. Y yo quiero que venga Pablo, así que votaré a 5ºB.

—Me parece muy bonito —añadió Ven con mucha pena y con la barbilla temblona —Eres la única persona que he visto todos los días de mi vida… y prefieres votar a Pablo antes que a mí…

El gafotas se quedó serio por un instante, luego añadió:

—De todas formas, Ven, yo no te puedo votar a ti, sino a tu clase. Eso no te asegura que seas tú uno de los elegidos.

—Ya lo sé, lo explicó la directora —dijo Ven hipando —Pero cuantos más votos tenga mi clase, más niños podrán ir de ella. Es como lo del concierto de los diputados.

—No me digáis que los diputados van a dar un concierto —Mati acababa de llegar —¿Será de rock?

—Hola, Mati —dijo Sal esbozando una leve sonrisa —Creo que Ven quería decir congreso, no concierto —y añadió poniendo la mano sobre el hombro de su hermano —¿verdad, Ven?

El pequeño asintió levemente con la cabeza, mientras usaba la manga derecha de su camiseta a modo de pañuelo para secar una lagrimita que resbalaba por su mejilla… y algún moquito también…

—Hola, Mati —se atrevió a susurrar finalmente Ven.

—¿Qué te pasa, cielo? —preguntó Mati —¿Por qué tanta pena?

—Porque Sal quiere más a Pablo que a mí…

—Eso no es cierto y lo sabes, Ven —protestó el gafotas —Además, aún no tengo decidido mi voto del todo, ¿sabes?

—Bueno, bueno… —intervino la pelirroja —¿Me contáis de qué va esta campaña electoral?

—Es que esta semana vienen al estadio olímpico los jugadores de la selección con la copa del mundo —empezó a contarle Sal —En nuestro colegio van a seleccionar a 32 niños para ir a verlos, y lo vamos a elegir como lo hacen los mayores para que todos los niños aprendamos sobre el sistema electoral de nuestro país.

—Sí, lo de la leydón —añadió el pequeño.

—¿La ley D’Hondt? Hala, qué buena idea… —dijo alegremente Mati —Me parece estupendo, algunos mayores no entienden cómo funciona la ley D’Hondt. Está bien que se aprenda en el colegio, sí.

—Bueno, Mati —aceptó el gafotas —yo tampoco sé cómo funciona, nos la van a explicar cuando cuenten los votos…

—¿Queréis que os la explique un poco? —preguntó Mati tratando así de relajar el ambiente que parecía un poco enrarecido.

—Vale —aceptó el pequeño.

—¡Sí! —pidió Sal —¡Por favor!

—Primero me tenéis que contar cómo es la votación, para que yo os explique cómo se gestionarán los votos.

—¿Se lo cuento yo, Ven? —preguntó Sal a su hermano en tono muy cariñoso tratando de disipar cualquier duda sobre el cariño que le profesaba a éste.

El pequeño asintió con su cabeza.

—Verás, Mati —empezó a contar Sal —Cada clase de segundo y tercer ciclo de primaria, es como un partido político: 3ºA, 3ºB, 4ºA, 4ºB, 5ªA, 5ºB, 6ºA y 6ºB.

—¿Los más pequeños no van? —preguntó la gafotas.

—Sí, pero ellos se eligen de otra manera más de pequeños, ¿sabes? —dijo Ven.

—Cada niño de segundo y tercer ciclo de primaria —siguió el gafotas —sólo puede votar a una clase, pero no a la suya…

—Y Sal quiere votar a la de Pablo… —masculló Ven.

—Cuando acabe la votación —siguió Sal como si no hubiese escuchado a Ven —se elegirán tantos niños de cada clase como indique la ley ésa.

—La ley D’Hondt —dijo Mati — D, apóstrofo, h, o, n, d, t…

—Toma, yo creí que era leydón porque era una ley muy importante… —intervino el pequeño.

Mati sonrió y continuó:

—Así que tenemos que elegir a 32 niños, como si fuesen 32 diputados…

—Diputado es una palabra con taco —interrumpió, de nuevo, Ven.

—Ven, no interrumpas tanto, por favor —le pidió Sal amablemente.

—Es que como estoy tan triste… —respondió Ven llevando el chantaje fraternal al extremo.

—Así que tenemos que elegir a 32 niños, como si fuesen 32 diputados, —repitió Mati en un tono un poco más elevado —de un conjunto de… ¿cuántos niños sois en total en esos cursos?

—No lo sé, Mati —reconoció Sal.

—Bueno, vamos a hacer una simulación —les propuso —Supongamos que hay 20 niños por curso, son 8 cursos, en total, 160 niños, ¿os parece?

Los dos hermanos asintieron con la cabeza. Gauss también, se ve que estaba de acuerdo.

—Os voy a contar el sistema que Victor D’Hondt propuso para obtener el número de diputados de cada partido, en función de los votos obtenidos.

—¿Era matemático? —preguntó Sal.

—Sí, también era matemático —respondió ella —Además de abogado, profesor de Derecho, hombre de negocios…

—Qué tío… —exclamó Ven.

—Vamos a inventarnos una tabla con los posibles resultados de las votaciones para explicar el sistema D’Hondt —les propuso.

—Vale —dijo Sal.

—Yo voto a 6ºA que es la clase de mi hermano… —dijo el pequeño remarcando mucho el final de su frase. Sal le miró de reojo con cierta resignación….

—Vamos a pensar que tenemos que elegir sólo 8 niños para la excursión al estadio, ¿vale? —propuso Mati

—¡Sí, claro! —protestó Ven.

—No te pongas así, Ven —le dijo ella —es sólo para hacerlo más corto. Para 32 se hace igual, pero más largo.

—Vale —aceptó el pequeño.

—Vamos a repartir los 160 votos entre las 8 clases —les propuso —Por ejemplo así —y les entregó una hoja de papel

Los niños miraron los votos de cada clase y aceptaron los resultados.

—Ahora, en la pizarra —continuó Mati —vamos a ir rellenando una tabla, como veis. Debajo de los resultados de cada partido político, perdón, de cada clase, escribimos el resultado de dividir sus votos por 1, 2, 3, 4, 5, 6, 7 y 8, ya que vamos a elegir a 8 diputados, digo, excursionistas en total.

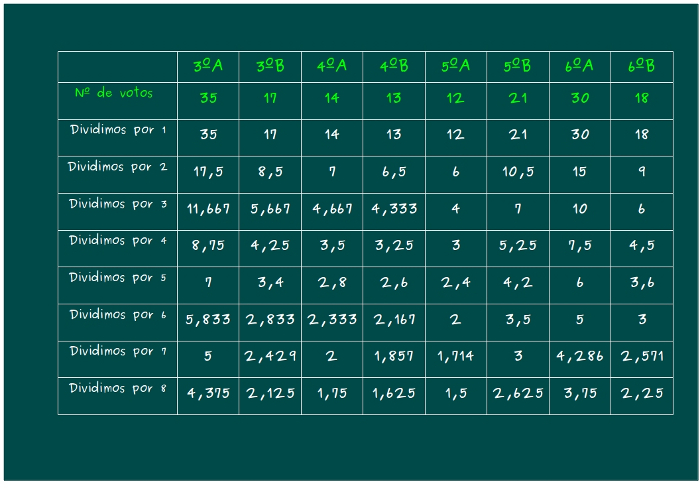
—Pues bien, chicos —les dijo —siguiendo el sistema D’Hondt, los 8 elegidos para la excursión, saldrán de los 8 valores más altos de todos los contenidos en esa tabla, los escritos en color blanco.

—¿Cómo? —preguntó Ven.

—Lo haremos uno a uno —contestó Mati —El primer diputado elegido, digo, el primer niño elegido corresponde a la casilla con el valor más alto, ¿cuál es?

—¡Ésta! —señaló Sal —El 35.

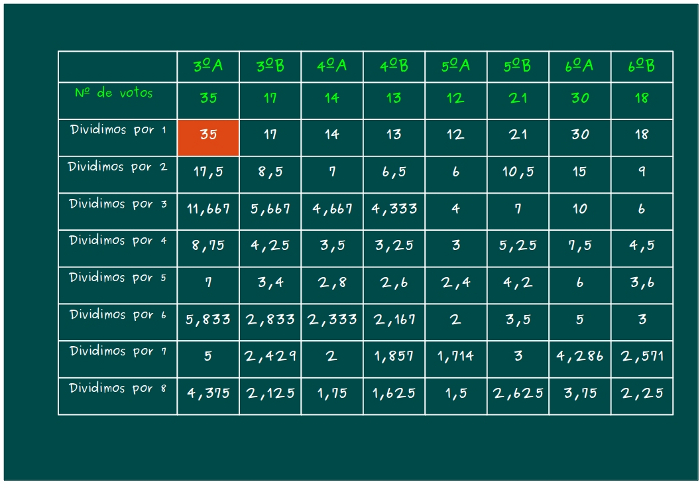
—Bien —dijo Mati —eso significa que el primer niño saldrá de la clase de 3ºA.

—¡Mola! —exclamó Ven.

—Vamos a por el segundo candidato —les propuso —¿cuál es el siguiente número más alto en la tabla?

—¡El 30, de 6ºA! —respondió el gafotas con alegría.

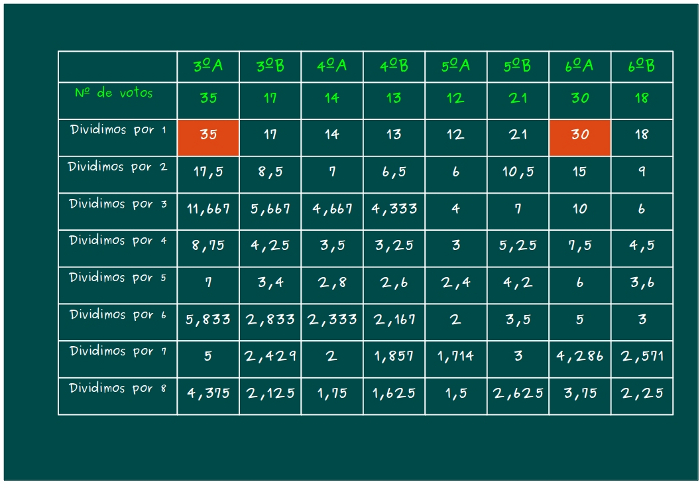
—Ajá —corroboró ella —El segundo niño será de la clase de 6ºA.

Sal sonrió feliz. Ven trató de disimular su alegría.

—¿Cuál será el siguiente? —volvió a preguntarles.

—¡Mira, Sal! —gritó Ven —Es el 21, y es de 5ºB, puede que vaya Pablo también.

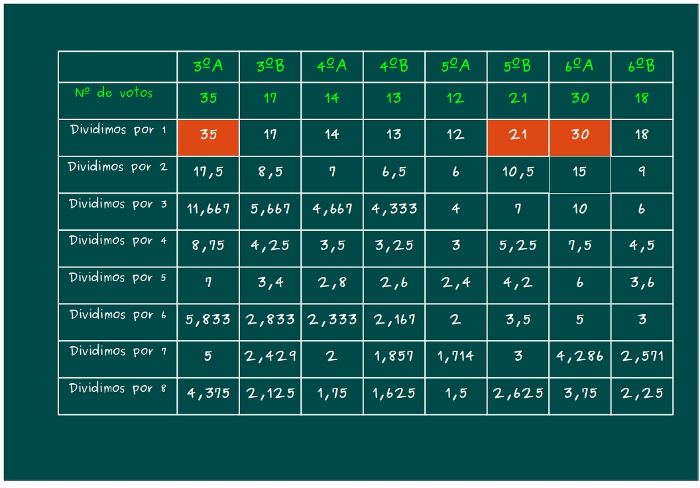
—Ven, esto es una simulación —le recordó su hermano con una sonrisa.

—¿Seguimos, chicos? —preguntó Mati

—El siguiente número es el 18 —dijo Sal —O sea, un candidato de 6ºB.

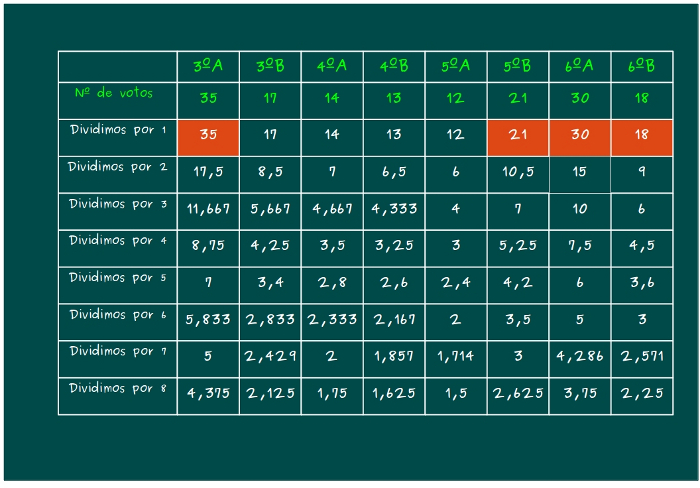
—El siguiente número más grande es …—dijo Ven —el 17’5, ¡toma, toma, toma!¡Otro de mi clase!

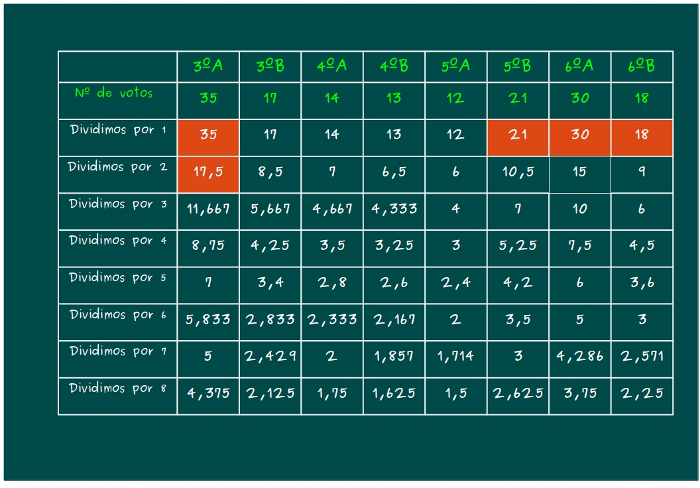
—Y ahora… —dijo Sal —es el turno del… 17, ¡un chico de 3ºB a bordo! —añadió cómicamente.

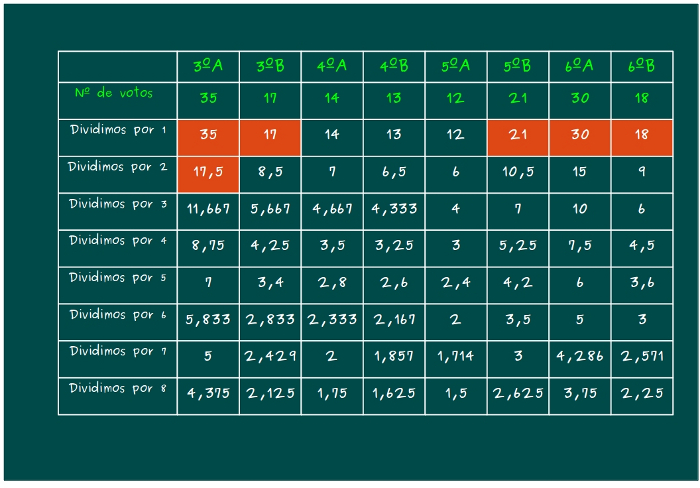
—¡No me lo puedo creer! —dijo Ven —El siguiente número es el 15, ¡otro de la clase de mi super hermanito!¡Cómo molaaaaaaaaaaa! —Ven se ponía casi de rodillas celebrándolo.

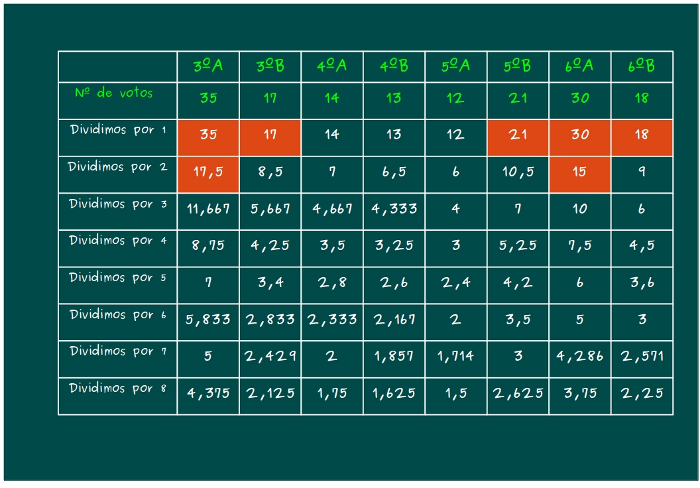
—Y el uĺtimo escaño, digo, la última plaza para la excursión…—decía el gafotas —con el número 14, ¡adjudicada a la clase de 4ºA!

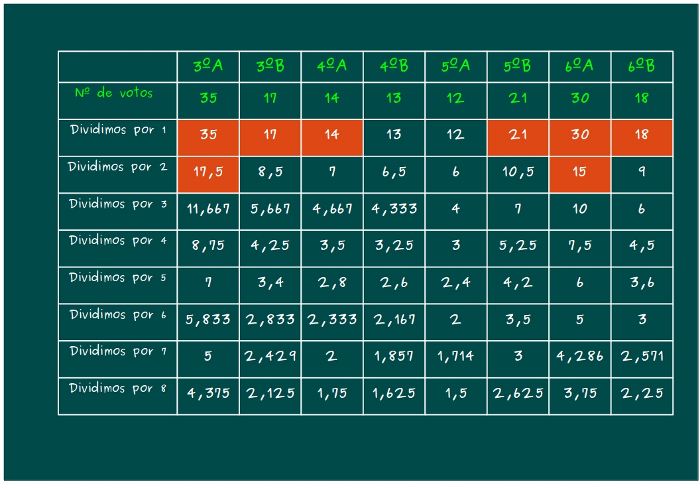
—¿Veis? —les dijo Mati —Ya hemos elegido a los 8 candidatos según D’Hondt, de forma proporcional al número de voto obtenidos: 2 alumnos de 3ºA, 2 de 6ºA, y un alumno de cada una de las clases de 3ºB, 4ºA, 5ºB y 6ºB

—¡Toma, toma, toma! ¡Cómo mola! —dijo Ven —Nuestras clases han sacado 2, Sal.

—Que es una simulación, Ven —aclaró el gafotas —Oye, Mati, y para elegir a los 32, ¿hay que añadir filas hasta dividir todos los resultados de los partidos por 32?

—No, no hace falta, es lo bueno de este sistema, ¿sabes? —respondió Mati —Podemos seguir eligiendo diputados, digo, excursionistas hasta que lleguemos al final de una de las columnas. En nuestra tabla, hasta que lleguemos al final de la columna de 3ºA, donde tenemos 4’375. Por lo tanto, con esta misma tabla podemos elegir tantos candidatos como números mayores que 4’375 hay en ella, ¿cuántos hay?

Los niños se pusieron a contar… Gauss seguía intentando parecer poco interesado en el tema.

—Hay 31 números mayores que 4’375, Mati —dijo finalmente Sal.

—En ese caso —respondió ella —nos sirve para elegir a 32 excursionistas…

—¡Toma, toma, toma! ¡Este Victor cómo mola, se merece una ola! —Ven estaba entusiasmado, tanto que olvidó su pequeño enfado con su hermano.

—¿Sabes, Ven? —dijo entonces Sal —Voy a votar a tu clase, me lo paso muy bien contigo.

—Espero que tengáis suerte, chicos —dijo Mati —Y a ver si convencemos también a nuestros amigos para que nos voten a nosotros, ¿no?

FIN

Pues sí, esta es la famosa Ley D’Hondt, aunque tengo que decir que sería más correcto llamarle Sistema D’Hondt o Método D’Hondt, porque se trata de un método, pero es popularmente conocida con el nombre de ley D’Hondt.

No es esta la primera vez que hablamos de votaciones y procesos electorales, os recomendamos que veáis este capítulo.

Si te gusta nuestro blog, puedes votar por él en la categoría de Educación de los Premios Bitácoras 2012

Muchas gracias

MATI