Un gran premio a 31 vueltas

—Esto se pone emocionaaaaanteeee… —retransmitía Ven con voz de locutor —estamos en la vuelta número 31 y Venttel va en primera posicióóóóóóóónnn… Pobre, Shalmacher… no podrá adelantarlooooo…

—¿Puedes jugar calladito, Ven? —protestó el gafotas —Y no me llames Shalmacher, pesado…

—Te llamaré Salmiltooooooooon… —Ven siguió restransmintiendo sin mirar a su hermano —¡Toma, toma, tomaaaaaaa! ¡Bandera de cuadros para Venttel!

Ven soltó el mando y abrazó a Gauss con más ímpetu del que éste hubiese preferido.

—Yo no juego más —dijo Sal soltando su mando —Esta pista es muy fácil y aburrida.

—¿¿Cómo?? —Ven miraba a su hermano con los ojos abiertos de par en par —Claro, como te gano siempre dices que esta pista es aburrida, ¿no?

—No es por eso… —trató de defenderse Sal.

—Pues que sepas que esta pista es la mejor —siguió argumentando el pequeño —porque se parece al infinito, y ¡el infinito es la caña!

—Bueno, no sé si es una caña el infinito —Mati acababa de entrar en el salón —A mí me recuerda a una rosquilla…

—¡Hola, Mati! —saludaron los dos hermanos.

—Hola, chicos —respondió la pelirroja —no pude evitar la tentación de entrar, me llegaba el olor a neumáticos y escuchaba la emoción del locutor…

—Bueno, ya sabes, Mati —dijo Sal sonriendo —Ven es un poco novelero para estas cosas…

—Y tú un poco tramposo —añadió Ven —¿Sabes, Mati? Como no me puede ganar nunca dice que esta pista es muy aburrida.

—Es que lo es… —insistió el gafotas.

Mati se quedó mirando el circuito muy pensativa, lo levantó por un lado, comprobó la resistencia del materíal, las conexiones de los raíles…

—Es una pena que no se pueda moldear un poco la pista —dijo finalmente.

—¿Moldear? ¿Para qué?

—Porque si, al menos, pudiésemos girar un poco uno de los tramos, Ven —contestó ella —tendríamos una banda de Möbius y eso sí que sería una pista alucinante…

—¿Una banda de qué, Mati? —preguntó rápidamente Sal.

—Una banda de Möbius —les contó —es una superficie con una sola cara y un solo borde.

—No entiendo, Mati —se quejó el pequeño.

—Verás, vuestra pista tiene 2 caras, ¿verdad? La de arriba, por donde corren los coches, y la de abajo —empezó a decir Mati —Para pasar de la cara de arriba a la de abajo, tendríais que levantar el coche de la pista o circular por el borde de la misma, ¿no?

—¡Toma, claro! —confirmó Ven.

—Pues bien, si la pista fuese una banda de Möbius, se podrían recorrer las dos caras, sin levantar el coche y sin pisar el borde —continuó Mati —porque en realidad, sólo tiene una cara.

—¡Ja! No me lo creo… —insistía Ven.

—Vamos a verlos con una cinta de papel y un lápiz, ¿queréis?

—¡Sí! — contestaron los dos niños.

Mati tomó una hoja de papel y cortó dos tiras rectangulares, más o menos iguales.

— Con esta primera tira vamos a hacer lo siguiente: —les propuso —Pegamos los dos extremos de esta tira, en la dirección que indican las flechas… y lo que nos queda es un cilindro.

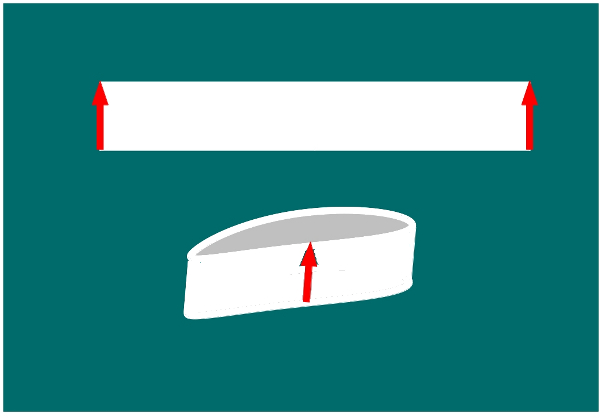
—Con esta otra tira, pegamos los bordes, pero girando uno de los extremos, como indican las flechas. Nos queda una banda (o cinta) de Möbius.

—Eso tiene dos caras, Mati…. —dijo Ven receloso.

—No, tiene sólo una —dijo la pelirroja —A menos que la veamos en dimensión 7 o superior, la banda de Möbius tiene una sola cara.

—¿En dimensión 7? —preguntó rápidamente el gafotas —¿Cómo se puede ver en dimensión 7, Mati?

—Huy, con el poder de la mente… —Mati le guiñó un ojo —Pero vamos a quedarnos en dimensión 3, ¿me prestáis un lápiz?

Ven le dio un lápiz a su amiga.

—Empieza a pintar con un lápiz empezando desde cualquier punto de la cinta de Möbius y trata de recorrerla entera —dijo Mati —verás que vuelves al mismo sitio y la cinta está pintada por los dos lados.

Sal y Ven construyeron una banda de Möbius cada uno y se pusieron a pintar como les había pedido Mati.

—¡Toma, toma, toma! —gritó Ven —¡Es verdad!

—Este hecho, —continuó Mati —el de que la cinta de Möbius sólo tiene una cara, se aprecia mejor en este dibujo de Escher.

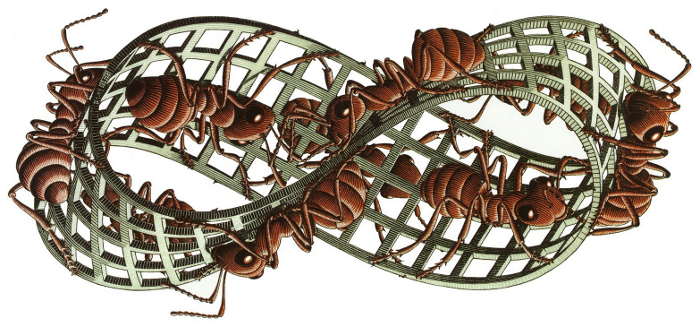
—¡Wow! —exclamó el gafotas —Es alucinante…

—¿Os imagináis una pista de coches así? —les preguntó la pelirroja.

—¡Hala! —exclamó el pequeño —¡Sería chulísima!

—Efectivamente, lo sería —corroboró Mati —Pero ya que tenemos las tiras de papel vamos a jugar un poco más con la banda de Möbius.

—¡Venga! —dijo el pequeño.

—Si cortamos el cilindro por la mitad, longitudinalmente —les dijo —tendremos dos cilindros.

Los niños cortaron un cilindro por la mitad y comprobaron lo que decía Mati.

—Pero si hacemos lo mismo con una banda de Möbius —les dijo —Nos queda una sola figura.

Los niños cortaron una cinta de Möbius por la mitad y descubrieron que les quedaba una sola pieza en las manos.

—¡TOMA! —gritó Ven —¡Ahora tenemos una banda de Möbius grandota!

—No, Ven —le corrigió Mati sonriendo —Eso que tenéis en las manos no es una banda de Möbius, tiene dos caras, comprobadlo con el lápiz.

Sal dibujó una linea a lo largo de la pieza obtenida tras cortar longitudinalmente la banda de Möbius y descubrió que, efectivamente, una de las caras de la cinta seguía sin pintar.

—¿Veis? —les peguntó Mati —No es una banda de Móbius, es un cilindro.

—Alucina, Sal… —Ven estaba muy emocionado.

—Pues fijaos, ahora —les propuso —si pintamos dos líneas paralelas a lo largo de la cinta de Móbius y cortamos…

—¡Saldrá un cilindro enorme! —se apresuró a decir Ven.

—Hacedlo —les retó Mati.

Los niños se pusieron manos a la obra…

—¿Esto qué es, Mati? —preguntó Sal —¿Son dos cilindros?

—No —les respondió ella —El más grande es un cilindro, pero el más pequeño es, de nuevo, una banda de Möbius.

—¡Es chulísimo, Mati! —dijo el pequeño.

—Lo es —confirmó ella —¿Queréis que os enseñe a hacer algo muy romántico?

—¡Oh, sí! —respondió Ven con cara de pícaro —Para Sal y Verónica...

—Calla, Ven —interrumpió Sal con las mejillas encendidas.

—Construimos dos bandas de Möbius —les dijo —Las pegamos de forma que una quede perpendicular a la otra. Cortamos cada una de las bandas de Möbius por la mitad y… vamos a verlo en este vídeo de nuestro amigo Joaquín

—¡Toma! —gritó Ven —Son dos corazones, el de Sal y el de…

—¡Calla, Ven!

—Es un regalo perfecto —añadió Mati —si además se acompaña de esta música que, según me contó Fis, le recuerda siempre a la banda de Möbius.

FIN

Pues sí, amigos, la banda o cinta de Möbius tiene un montón de propiedades maravillosas. Si queréis conocer más, os aconsejo que echéis un vistazo a este trabajo muy completo de Marta Macho Stadler, del que además hemos tomado prestadas algunas fotografías de nuestra mateaventura.

A mí me gusta mucho porque, además, es la imagen de los blogs de dos de mis mejores amigos: Tito Eliatron y Gaussianos.

¡Hasta dentro de dos semanas!

MATI