Una línea de 22 centímetros

— La primera etapa mide 22 centímetros de largo. Ven, dibuja una línea de 22 centímetros, sin doblarte, por favor.

—Sin doblarme, sin doblarme… —repetía el pequeño en voz baja mientras trataba de dibujar la línea en la cartulina —Creo que no va a caber en esta cartulina…

—Pero, Ven, ¿cómo no va a caber una línea de 22 centímetros en una cartulina?

—Pues no cabe, Sal, fíjate que se sale… —dijo Ven marcando con el escalímetro sobre la cartulina desplegada en la mesa.

Sal se acercó ajustándose las gafas sobre la nariz.

—Pero, Ven, ésos no son centímetros, dale la vuelta a la regla, ¡por Euler! ¿Cómo vamos a conseguir que este cohete despegue si no pones bien las medidas?

—Toma, es verdad, ¡qué fallo más tonto! —contestó el pequeño llevándose las manos a la cabeza —Con esta regla tan rara que has cogido…

—No es rara, se llama escalímetro.

—Es rara, Sal, me da igual cómo se llame.

—Ponla por el lado de 1:100 y pinta la línea de la primera etapa que no vamos a acabar nunca.

—Vaya, qué atareado os veo hoy, ¿alguna manualidad para el colegio? —Mati había llegado.

—¡Hola Mati! —Ven soltó la regla rara y junto con Gauss fueron a abrazar a la recién llegada.

Sal se acercó también mirando aún de reojo el plano que dejó sobre la mesa.

—Hola, Mati —la saludó —No, no es para el cole. Es que queremos construir un cohete.

—Bueno, bueno… eso sí que es una misión difícil y emocionante para mis científicos… —dijo la pelirroja con voz afectada.

—En realidad hoy no somos científicos somos ingenieros aeroespaciales —respondió el pequeño hinchando el tórax.

—Ingenieros aeroespaciales que no saben medir bien… —dijo Sal con picardía.

—Chivato… —masculló Ven —No me gusta esa regla y punto.

—¿El escalímetro? —preguntó Mati —Bueno, es una regla muy cómoda para dibujar a escala, pero sí, para vuestro cohete no hace falta posiblemente.

Ven miró a Sal de reojo y retorció la boca en señal de victoria. Mati continuó.

—Hablando de reglas raras o especiales, ¿habéis oído hablar de las reglas de Golomb?

—¿Reglas de Gollum? ¿El de la Tierra Media? —preguntó Ven con cara de pillín.

—No, de Golomb —repitió Mati sonriendo — Son unas reglas muy originales en las que no están puestas todas las marcas.

—Lo que faltaba, así sí que no acabaremos nunca el cohete… —se lamentó Sal.

—No, efectivamente, para el cohete es mejor que uses una regla estándar. Pero las reglas de Golomb tienen muchas utilidades, por ejemplo, para minimizar interferencias entre bandas de radio o incluso para maximizar la recepción en los radiotelescopios que investigan el espacio.

—Toma, mola… —Ven ya estaba atrapado en las redes de Mati.

—¿Qué tienen de especial esas reglas, Mati? —preguntó el gafotas.

—En una regla de Golomb sólo escribimos algunas marcas, pero no de cualquier manera, si no de forma que las distancias entre cualquier pareja de marcas no se repitan.

Ante la cara arrugada de los niños, Mati continuó

—Por ejemplo, consideramos una regla de 8 centímetros y marcamos sólo dónde está el 1, el 5, el 7 y el 8, cómo en ésta de la pizarra.

—Vamos a ver si efectivamente se trata de una regla de Golomb, calculando todas las distancias posibles entre 2 marcas distintas. Si no se repite ninguna distancia, lo tenemos.

—¿Podemos hacerlo nosotros, Mati? —preguntó alegre Ven.

—Claro, calculad la distancia de cualquier marca al 1, para empezar.

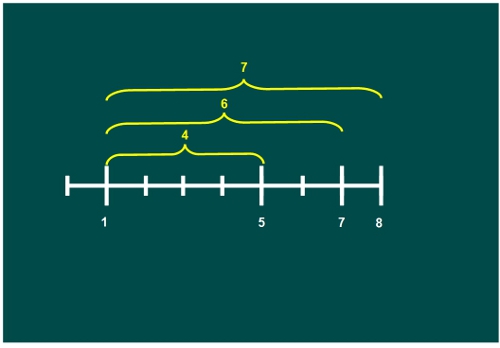
—Ya está, lo tenemos, 4, 6 y 7 —afirmó Sal.

—Muy bien, chicos —dijo la gafotas —Ahora las distancias entre el 5 y las otras marcas, excepto el 1 que ya la hemos medido.

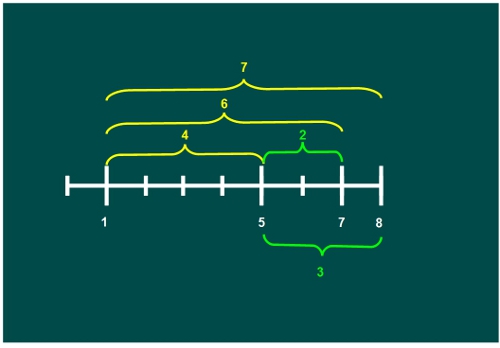
—¡2 y 3! —contestó Ven con ímpetu.

— Nos queda el 7 con el 8 y terminamos —dijo Mati.

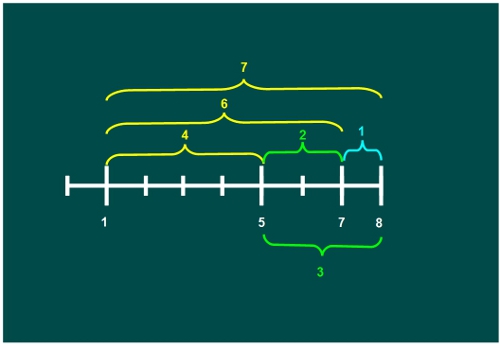
—Ésa está chupada —afirmó Ven —¡1!

—Pues sí, Mati —continuó el gafotas —Todas las distancias son distintas. Es una regla de ésas.

—Efectivamente, chicos —corroboró ella —Es una regla de Golomb. Al número de marcas de la regla le llamamos orden de la regla. Ésta es una regla de orden 4. Y llamamos longitud de la regla a la diferencia entre la primera y la última marca. La nuestra es una regla de longitud 7. Aunque lo habitual es construir reglas de Golomb con una marca en el 0 y otra en el final. Ahora os pregunto, ¿podemos dibujar líneas de cualquier longitud entre 1 y 7 con esa regla?

Los niños se quedaron mirando la pizarra de Mati.

—Tenemos 1, 2, 3, 4, 6 y 7 … —mascullaba Sal —Nos falta el 5, Mati.

—Eso es, por eso esta no es una regla de Golomb perfecta. Las reglas de Golomb perfectas son las que nos permiten, usando las marcas en ella, medir cualquier distancia entre 1 y el total de la longitud de la recta. Os voy a dibujar una de longitud 6.

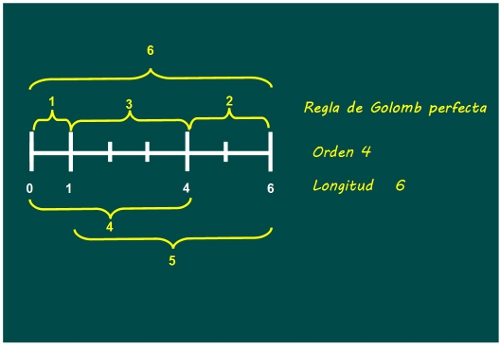
—¡Toma, toma, toma! ¡Cómo mola! —Ven estaba entusiasmado.

—¡Vamos a construir otra regla perfecta, Mati! —pidió Sal muy emocionado.

—Bueno, bueno, Sal —trató de calmar Mati —No es nada fácil construir reglas perfectas. De hecho, no existen reglas de Golomb perfectas con más de 4 marcas.

—¿Seguro? —preguntó Ven desconfiado.

—Segurísimo —respondió Mati cómicamente —Se ha demostrado que no existen reglas de Golomb perfectas con más de 4 marcas.

—Vaya rollo… —se quejó el pequeño desilusionado.

—Pero se puede jugar a construir reglas de Golomb —lo animó Mati — aunque no sean perfectas. Aquí tenéis una regla de longitud 11 y unos rotuladores. Os reto a que construyáis una regla de Golomb con 5 marcas, señalándolas con el rotulador.

—Vale —aceptó Sal —¿Por qué se llaman así estas reglas? ¿Qué significa Golomb, Mati?

—Es el nombre de un matemático e ingeniero norteamericano, Solomon Golomb…

—Oh, cuántas oes… —masculló Ven.

—Sí, es verdad, Ven —respondió Mati sonriendo —Como ha sido Golomb quién más ha popularizado estas reglas, se les ha dado su nombre.

—En realidad, su apellido… —puntualizó Sal.

—Sí su apellido —confirmó Mati —Pero antes que la construcción de las reglas de Golomb, otro matemático, húngaro, había planteado un problema similar, Simon Sidon.

—Simon Sidon —dijo Ven canturreando —¡Qué nombre tan gracioso!

—¿Y bien? —continuó Mati — ¿Os atrevéis a dibujar 5 marcas sobre esta regla de forma que sea una regla de Golomb?

Los niños cogieron la regla y el rotulador que Mati les ofrecía y se pusieron manos a la obra.

—La primera y la última hay que marcarlas, ¡eso está claro! —el pequeño Ven estaba intrigado.

—Sí, Ven… —respondió su hermano —Es lo que acaba de decir Mati…

—Si queréis, podéis usar mi pizarra para ir anotando las diferencias entre todas las parejas de marcas para comprobar que no se repita ninguna.

—Sí, gracias, Mati —respondió Sal —Entre la primera y la última, mide 11. Lo apuntamos.

—Ahora marca el 1, Sal, que sale 1 y 10. Ésas no están repetidas.

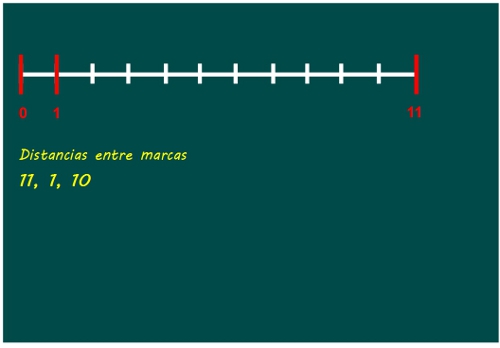
—Ahora el 2 no lo podemos marcar porque está a distancia 1 del 1… —pensaba Sal en voz alta —Marcamos el 3 y a ver qué pasa.

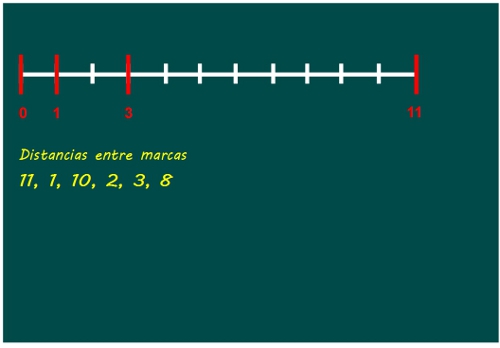
—¡Qué caña, Sal! —Ven abrazó a su hermano excitado —sólo nos falta poner una marca.

—Sí — respondió orgullos el gafotas — En el 4, no puede ser, porque se repiten el 3 que es la distancia al 1, y el 1 que es la distancia al 3…. En el 5 tampoco porque se repite la distancia 2 con el 3…

Sal y Ven escribían en la pizarra las distintas posibilidades para la cuarta marca que debían poner y marcando en rojo las distancia que se iban repitiendo.

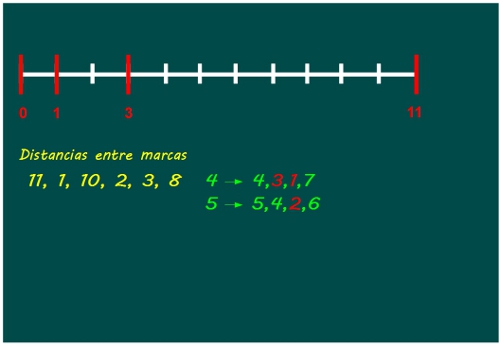
—Probamos con el 6…nos sale el 3. Probamos con el 7… nos sale el 4 dos veces. El 8…tampoco. El 9… tampoco. Y el 10…¡TAMPOCO!

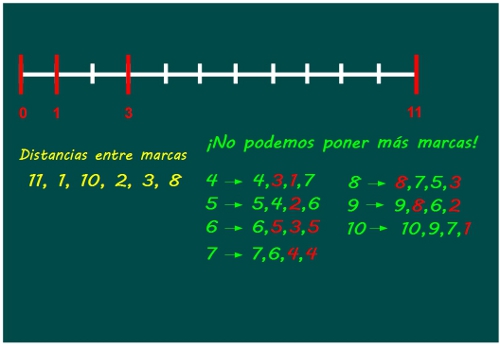
—¡Es imposible, Mati! —gritó Ven desesperado.

—¿Por qué? —respondió ésta —A lo mejor es que habéis puesto una que no es…

—Claro. Vamos a quitar el 3 y ponemos el 4, a ver qué pasa. A lo mejor nos equivocamos al poner el 3.

—¡Quita el 3, quita el 3! —Ven se estaba poniendo cada vez más nervioso.

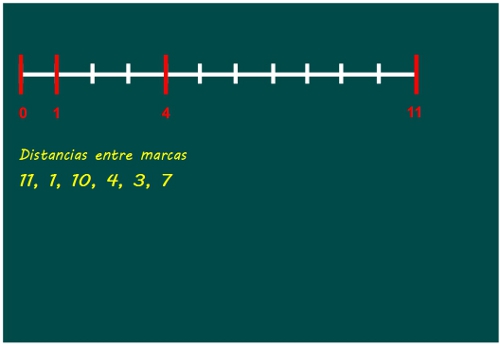
—Vamos a ver dónde ponemos la quinta marca, Sal.

—El 5 no vale… el 6 tampoco…ni el 7…ni el 8… —Sal calculaba las distancias de las posibles marcas a las cuatro ya puestas y señalaba en rojo las que se repetían.

—Joooooo —El corazón de Ven se aceleraba cada vez más.

—¡El 9!¡El 9! —gritó Sal de repente.

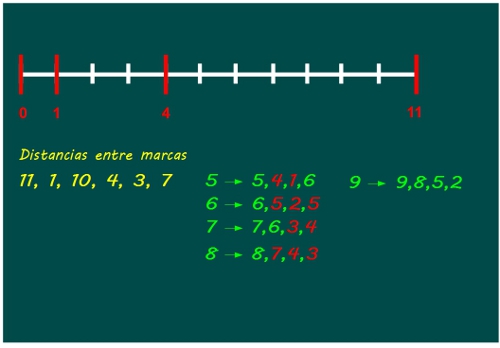
—¡Oé, oé, oé! —Ven daba vueltas alrededor de Sal y Mati como quien celebra un gol.

—¡Bravo! Ya tenéis vuestra regla de Golomb de longitud 11 y con 5 marcas —Mati sonreía satisfecha.

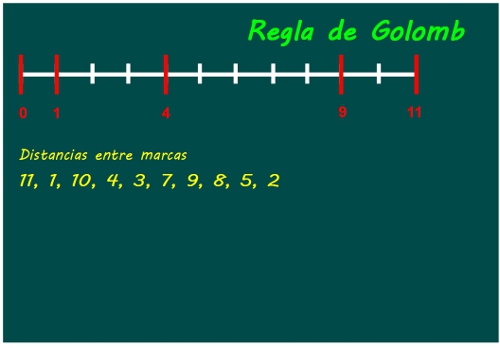
—¡Toma, toma, toma! ¡Cómo mola!¡CÓMO MOLA! —Ven no podía quedarse quieto de la emoción.

—¿Hacemos otra, Mati? —preguntó Sal nervioso.

—No, ahora, como veo que esto lo domináis tan bien. Os voy a proponer un reto más difícil, con grafos.

—¡Me gustan los grafos! —afirmó Ven.

—El problema similar al de las reglas de Golomb en grafos consiste en poner un número, una etiqueta en los vértices. Si dos vértices están unidos por una arista, a esa arista le ponemos como etiqueta la diferencia entre las etiquetas de los vértices, la mayor menos la menor. Pues bien, se trata de colocar numeritos en los vértices para que los números de las aristas vayan de 1 hasta el número total de aristas, sin repetirse y sin faltar ninguno. Si se puede hacer, a ese grafo se le llama grafo gracioso.

—¿Sí? ¡Qué gracia! —el pequeño Ven disfrutaba siempre con las invenciones de su amiga pelirroja.

—Ya veréis, este grafo es un grafo muy conocido, es el grafo de Petersen.

—Pues bien, chicos, este grafo es un grafo gracioso. Os atrevéis a poner las etiquetas.

—¡Vamos! —dijo Sal muy animado.

—Pon el 1 en el centro, Sal —animó Ven — y aquí arriba el 2.

—Vale, Ven, y esa arista tendrá 2 menos 1, etiqueta 1 —contestó su hermano.

—Aquí el 3, Sal —animaba el pequeño.

—No, porque entonces esa arista tendría 2 menos 3, 1, que ya está puesto —respondió Sal.

Los niños estuvieron dando vueltas al grafo poniendo y quitando números de los vértices de aquí y allá. Cuando comenzaban a desanimarse, Mati se ofreció a echarles una mano. Al cabo de un rato, ya habían etiquetado el grafo de Petersen como un grafo gracioso.

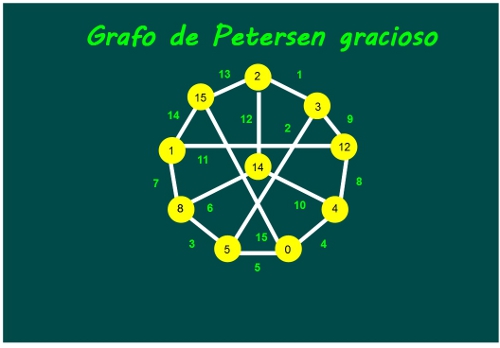
—¡Lo hemos conseguido, lo hemos conseguido! —el pequeño estaba entusiasmado.

—Éste era muy difícil, Mati —aceptó Sal.

—Sí, un poco más, pero es divertido, ¿no?

—Sí, es muy gracioso —dijo Sal con un guiño.

—Bueno, y ahora ¿queréis que os eche una mano con la construcción de vuestro cohete? —preguntó la gafotas.

—¡Sí! —contestó Ven que no llevaba muy bien trabajar a las órdenes de su hermano.

—¿Dónde pusiste el escalímetro, Ven?

FIN

Como ya se ha dicho antes, el problema de la construcción de reglas de Golomb fue planteado anteriormente por el matemático húngaro Simon Sidon, dando lugar a los conjuntos de Sidon que son lo mismo que la reglas de Golomb. Un conjunto de Sidon es un conjunto de números naturales con la propiedad de que la suma de cualquier pareja de éstos no se repiten. Los problemas relacionados tanto con conjuntos de Sidon como con reglas de Golomb no son nada sencillos de abordar. No hace mucho de hecho, dos matemáticos españoles fueron noticia por haber conseguido resolver uno de ellos.

Pues bien, si una regla de Golomb es perfecta cuando se pueden medir todas las distancias desde 1 hasta la longitud de la misma usando sus marcas, una regla de Golomb es óptima si es la más corta que se puede construir con ese orden, con ese número de marcas. Ya hemos contado que no existen reglas de Golomb perfectas con más de 4 marcas ¿Qué se sabe de las reglas de Golomb óptimas? Se han construido reglas óptimas de Golomb de hasta 26 marcas usando computación distribuida , es decir, utilizando un gran número de ordenadores trabajando a la vez. Si tienes interés en saber cómo va la búsqueda de reglas de Golomb ótimas con 27 marcas, lo podés ver aquí y si te animas, puedes colaborar aportando tu ordenador a este proyecto de computación distribuida.

Antes de despedirme os voy a proponer algo que podéis intentar hacer en casa sin necesidad de muchos ordenadores, sin más que un lápiz y papel. Ya habéis visto cómo Sal y Ven han construido una regla de Golomb de longitud 11 con 5 marcas, (0, 1, 4, 9, 11) ¿Os atrevéis a construir una regla de Golomb de longitud 17 y 6 marcas? Te pongo las 2 primeras, sólo tienes que añadir 4.

¿Y una regla de Golomb de longitud 25 y 7 marcas? También te pongo las dos primeras, sólo faltan 5.

Ya me diréis en los comentarios dónde hay que colocar las marcas que faltan en estas dos reglas para que sean de Golomb.

Hasta pronto

MATI