Si te digo veintiún mililitros, son 21 mililitros

—Ahora, 21 mililitros de colorante verde, Ven.

—Vaya, esta vaso de precipitado no tiene esa marca… pero yo creo que esto son más o menos 21 mililitros.

—¡¿Cómo que más o menos?! Pero, ¿qué clase de científico puede decir más o menos? Tienen que ser exactamente 21 mililitros, nada de más o menos, Ven.

—Es que no está marcado, Sal, y si esto son 25 mililitros —se defendió el pequeño Ven señalando con su dedito al vaso —por aquí, más o menos, debe ser 21 mililitros.

—¡Otra vez más o menos! ¿Sabes, Ven? ¿Sabes quién es el padre de la química moderna? —respondió Sal con vehemencia y añadió —Te lo diré yo que estoy en quinto y lo estamos estudiando.

—Te lo diré yo que estoy en quinto —repitió Ven remedando a su hermano mayor.

—¿Quieres que te lo cuente o no? —respondió el gafotas.

—Venga, vale —aceptó Ven al que, en realidad, le encantaba aprender de su hermano.

—El padre de la química moderna era un francés llamado Lavoisier que fue el primero que se dio cuenta de la importancia de medir todo muy, muy bien cuando hacían los experimentos.

—Efectivamente, Sal —Mati acababa de entrar — Descubriendo, gracias a sus mediciones meticulosas, que la masa no se crea ni se destruye, aunque la materia se puede transformar cambiando de estado.

—¡Hola, Mati! —saludó Ven con alegría.

—Hola, Mati —saludó Sal todavía un poco alterado con el más o menos de su hermano —¿Cómo se llama esa ley? No me acuerdo ahora.

—Ley de conservación de la masa —respondió la pelirroja —¿Y cómo es que os encuentro hablando de Lavoisier?

—Porque estamos haciendo un experimento y Ven quiere poner las cantidades más o menos.

—¡Que no están marcadas en el vaso! —intervino Ven —Qué pesadito…

Sal miró a su hermano de reojo pero no dijo nada, entendía que siendo tan pequeño no llegase a comprender la suprema importancia de la precisión exigida en un experimento de tan elevado nivel. Gauss intentaba mantenerse al margen de la discusión, no tenía muy clara su postura. Fue Mati la que intervino para rasgar aquel silencio incómodo.

—Esto me recuerda…

—¡A un problema de matemáticas! —interrumpió Ven con alegría.

—Eso es —confirmó Mati con una sonrisa.

—¿Cuál? —preguntó Sal abandonando por un momento su experimento.

—Bueno, se trata de resolver un problema similar al que tenéis con el vaso. Pero con un masu.

—¿¿Un qué?? —preguntaron los dos hermanos con las caritas arrugadas como pasas.

—Un masu es una caja cuadrada de madera, sin tapa, que se usaba tradicionalmente en Japón para medir las cantidades de arroz.

—¿Ya no? —preguntó Ven.

—No, ahora principalmente se usa para beber sake, que al fin y al cabo también viene del arroz, o para poner en la mesa la sal, la pimienta u otras especias —contestó Mati —Pues bien, vamos a usar este masu que tiene capacidad para 6 litros.

—Es precioso… —dijo Sal cuando Mati le mostró el masu de madera.

—Sí, lo es, lo compré en un viaje a Japón —dijo ella —Es de madera de ciprés, como los tradicionales.

—¿Qué tenemos qué hacer con esta cajita, Mati? —preguntó ven impaciente.

—Os lo cuento. Este masu, esta caja, tiene capacidad o volumen de 6 litros. Queremos usarla para vender agua, por ejemplo, a nuestros clientes que nos pueden pedir cualquier cantidad de litros. Pero vamos a suponer que sólo nos piden una cantidad de litros comprendida entre el 1 y el 6.

—¿Pueden pedir litro y medio? —quiso saber Sal.

—No, litros completos solamente —respondió la gafotas — Pero hay más reglas en el juego. El agua la sacamos de un depósito grande usando el masu, pero sólo podemos coger agua del depósito una vez, aunque sí podemos devolver agua al depósito cuantas veces queramos. Nuestro cliente, también traerá un masu de este tamaño y tendremos que llenarlo con lo que nos pida, ¿me explico?

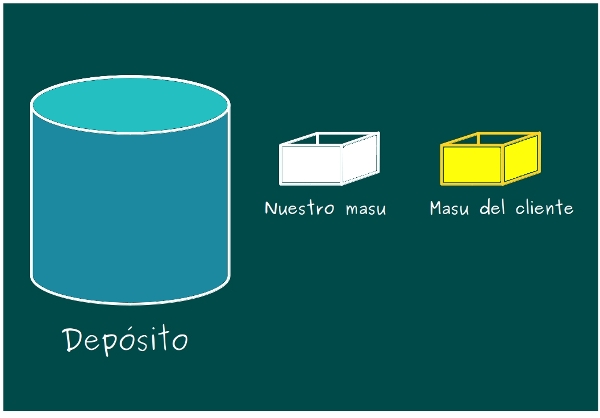
—Te explicas —respondió Ven.

—Entonces, ¿cómo venderíamos un litro con estas reglas?

—Ven, antes de que hables —dijo Sal —No digas “un litro es más o menos esto”.

Ven entrecerró los ojos y miró a su hermano, con los labios apretados. Pero al momento, los dos le daban vueltas y vueltas al masu para encontrar, si existía, alguna marca en la cajita que sirviera de pista. Pero no, no había ninguna marca.

—Ni idea, Mati —acabaron aceptando los dos científicos.

—A ver, dejadme que os explique un poco de geometría. El volumen, o capacidad, de esta caja que es un paralelepípedo —dijo Mati mientras Ven arrugaba la cara tratando de repetir aquella palabreja — se calcula multiplicando el área de su base por la altura.

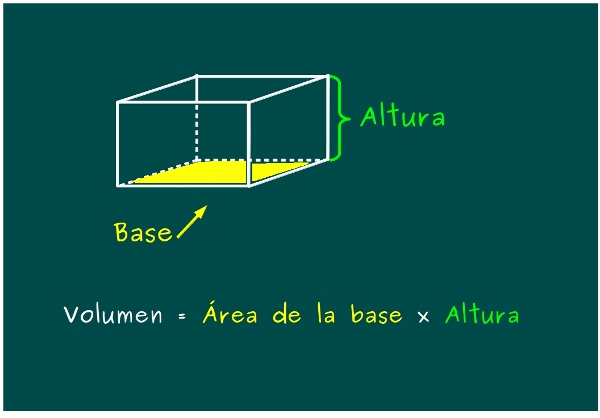
—¿Cuánto mide el área de la base de tu masu? —preguntó Sal.

—¿Y la altura? —añadió Ven.

—Esos datos no los vamos a necesitar, ya veréis, sólo necesitamos conocer el volumen, que en el caso de mi masu es de 6 litros.

—Mola —añadió el pequeño.

—Y bien, chicos, ¿cómo serviríais sólo un litro de agua al cliente sacando agua del depósito con este masu?

Los chicos dieron un par de vueltas más a la caja de madera buscando el truco, otra vez sin éxito.

—Nos rendimos, Mati —terminó aceptando Sal.

—Si llenamos el masu en el depósito, y lo volcamos vaciando el agua hasta que ésta quede alineada con uno de sus vértices, lo que nos queda es, exactamente, un litro. Así, como en este dibujo.

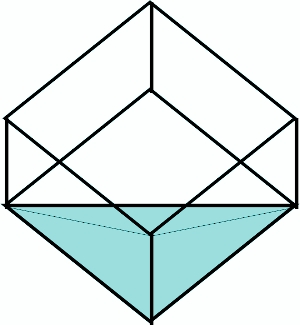
—¿Cómo la sabes, Mati? —preguntó Sal con los ojos de par en par.

—Vamos a calcularlo. El agua, así tal y como aparece en la figura, forma una pirámide, de base triangular ¿Sabéis la fórmula para calcular el volumen de una pirámide?

Los dos hermanos negaron con la cabeza. Gauss miró a otro lado.

—El volumen de una pirámide se calcula como el producto de la base, del área de la base, por su altura, divido por 3.

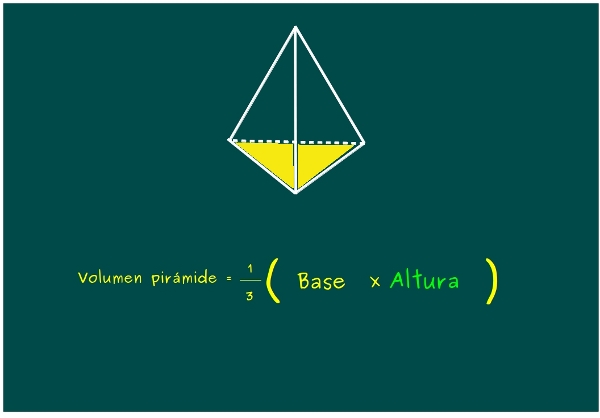
—En nuestra pirámide, la base es la mitad de la base del masu y la altura es la altura del masu. Si hacemos las cuentas, fijaos que sale.

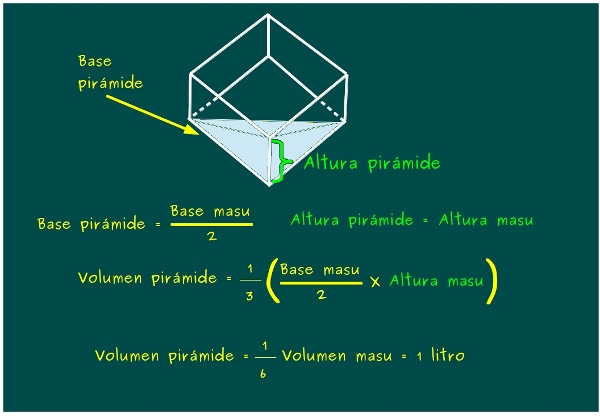
—¡Toma, toma, toma! ¡Cómo mola! —el pequeño Ven estaba entusiasmado.

—¡Qué chulo, Mati! —Sal también alucinaba con la solución.

—Me alegro de que os guste —dijo ella —¿Y 2 litros? ¿Cómo serviríais 2 litros?

—Muy fácil —comentó el gafotas —Basta con hacerlo 2 veces.

—¡MEC! ¡Error! —dijo Mati cómicamente — Sólo puedes sacar agua del depósito una vez. Las reglas son las reglas.

—Entonces, ¿cómo? —preguntó el pequeño.

—Os mostraré primero cómo obtener 3 litros que es más fácil —continuó la pelirroja —Para ello basta con inclinar la caja hasta hacerla coincidir con un lado de la misma, como en este dibujo.

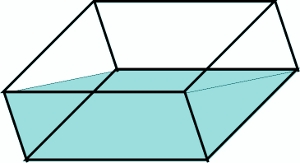
—¡Toma, claro! —gritó de repente Sal —Eso sería la mitad del masu, que como tiene 6 litros, serían 3 litros, ¿no?

—Muy bien, Sal —respondió Mati.

Ven, con cara de orgullo, le puso el brazo a su hermano por los hombros.

—Y ahora, ¿sabéis cómo servir 2 litros?

Los niños se quedaron pensando un rato, cuchicheando entre ellos. De pronto, un grito ahogado de Ven anunció la respuesta de éstos.

—¡Lo tenemos, Mati! —anunció el pequeño moviendo los brazos arriba y abajo.

—Sí —corroboró su hermano —Cogemos el masu lleno, con 6 litros, vaciamos 3 en el depósito como nos has enseñado, alineando el agua con un lado de la caja. Entonces tenemos 3 litros en el masu. Ahora volcamos el agua en el masu del cliente hasta que nos quede 1 en el nuestro, como nos dijiste al principio, alineando con el vértice. Le habremos puesto 2 al cliente y el que sobra, de vuelta al depósito.

—Pero, bueno…¡qué chicos tan listos!

— Somos científicos, Mati, no te olvides… —dijo Ven con cara de pillín mientras su hermano lo volvió a mirar de reojo recordando su más o menos.

—No me cabe duda de que seréis unos grandes científicos —respondió la gafotas —¿Os atrevéis con 4 litros?

Otra vez los niños montaron su gabinete secreto de medidas, cuchicheando y perpetrando la medida.

—Si cogemos 6 del depósito…podemos soltar 3 en el masu del cliente como antes, alineando con el lado… —dijo Sal.

—Nos quedarían 3 en nuestro masu… —apuntó su hermano.

—¡Ya está, Ven! —gritó Sal —Volcamos nuestro masu en el depósito hasta dejar sólo 1 litro alineando con el vértice.

—¡TOMA, TOMA, TOMA! —dijo Ven antes de agarrar la cara de su hermano con sus manitas y zamparle un beso.

—¡Maravilloso! —Mati no podía dejar de sonreír observando la escena.

—¡Somos unos cracks! —gritó un Ven entusiasmado.

—Y 5 es muy fácil, Mati —dijo Sal —Basta llenar nuestro masu con 6 litros y vaciar el agua en el del cliente hasta que en el nuestro sólo quede uno y ya está.

—Muy bien, Sal, muy bien —Mati sonreía sin parar, orgullosa de sus científicos.

—Somos tan científicos como el francés ese —dijo Ven ufano.

—Bueno, bueno… —dijo Sal —Lavoisier además de medir todo muy bien medido, fue el descubridor del oxígeno, ¿eh?

—Efectivamente —confirmó Mati —aunque hay que decir que fue gracias a los experimentos de Joseph Priestley

—¿El cantante de rock todo moderno? —preguntó Ven.

—¡Jajajajajajajaja! —Mati no pudo reprimir la carcajada —No, cielo, el todo moderno era Elvis Presley, Priestley fue, entre otras cosas, un químico inglés del siglo XVIII.

Ven se enfurruñó ruborizado por su flagrante confusión. Sal, intentando desviar la conversación propuso:

—¿Seguimos con los experimentos, Ven?

—Vale —dijo el pequeño y se dirigieron a su laboratorio.

—¡¡¡Oh, no!!! —gritó de pronto Sal —¿¿Qué has tomado, Gauss??

FIN

¿Qué? ¿Os han gustado los acertijos de medidas con el masu? Ahora os propongo otro con jarras de agua:

Dispones de tres jarras grandes con capacidades de 3, 5 y 8 litros. La jarra de 8 litros está llena de agua. Tu tarea consiste en medir exactamente 4 litros de agua. No dispones de otros recipientes para trabajar y los recipientes no tienen marcas que indiquen fracciones.

Estaré por aquí esperando vuestras respuestas en los comentarios.

Y si os queréis fabricar vuestro propio masu de papel, podéis aprender cómo en este enlace. Y si no os dejan en casa experimentar las medidas del masu con agua, podéis hacerlo con arroz.

Hasta pronto.

MATI