El oro estaba escondido en una estrella de 5 puntas

«—Personas refinadas y sofisticadas como nosotros no deben ensuciar sus labios con obscenidades.» —dijo Patricio a su amigo Bob, y se quedó tan pancho

Sal y Ven se deshacían en carcajadas, cosa que nada tenía que ver con lo que había dicho la estrella de mar, sino más bien con el hecho de que éste era el personaje favorito de los dos en la serie de Bob Esponja.

—Uf, ¡qué antipático es Calamardo! —se quejó con tristeza Ven.

—Es verdad, menos mal que Bob siempre trata a Patricio con cariño —le respondió su hermano.

— Por cierto, Sal, ¿todas las estrellas de mar tienen cinco puntas, una para la cabeza, dos para los brazos y dos para las piernas, como Patricio?

— Ven, es un dibujo animado…

—Ya lo sé —respondió Ven molesto —sólo quería saber si todas las estrellas de mar tienen 5 puntas.

—No todas, la mayoría sí, pero algunas no. —era Mati quien hablaba

—¿Hay estrellas de más de 5 puntas, Mati? —preguntó el gafotas

—Sí, por ejemplo, las de la familia  Solaster dawsoni

—Pues a mí me gustan más las estrellas de 5 puntas, como Patricio —sentenció el pequeño, mientras el gafotas se mostraba ilusionado. 

—Bueno, a mí también, Ven  —continuó la pelirroja —Las estrellas de cinco puntas, son muy importantes para los matemáticos.

—¿Por qué? —preguntaron los dos hermanos al unísono.

—Os cuento, la estrella de cinco puntas, llamada Pentagrama…

—El pentagrama son 5 líneas para escribir música, Mati —interrumpió Ven mosqueado —nos lo explicaron en clase.
 

—También, también se llama pentagrama, es cierto. Pero en geometría, un pentagrama es una estrella de 5 puntas como ésta:

—También se le llama Estrella Pitagórica,  porque  Pitágoras y sus discípulos la usaban como símbolo de su escuela. ¿Seríais capaces de dibujarla de un solo trazo, sin levantar el lápiz del papel?
 

Sal y Ven se pusieron manos a la obra. Fue el pequeño, Ven, el que antes lo consiguió y lo explicó con entusiasmo. 

—Mira, así —y dibujó en su cuaderno

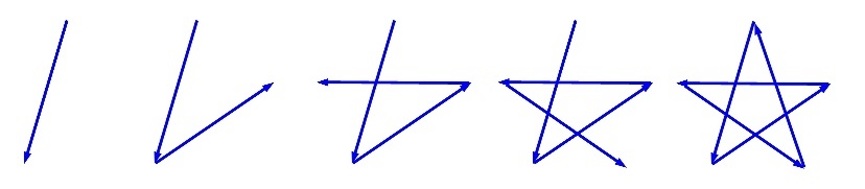
—¿Veis? Hay que dibujar 5 líneas, tiene 5 puntas y sin las puntas, nos queda un pentágono, que es un polígono con 5 vértices.

— Una estrella con muchos 5, la estrella de los aprobados raspones — bromeó Mati y les guiñó un ojo  —pero aparte del 5, el pentagrama esconde otro número más famoso e importante: el número de oro, que se escribe con la letra griega φ (o en mayúsculas Φ) (que se lee fi) 

—Otra letra griega, como π —señaló Sal con una sonrisa de oreja a oreja

—¡Ajajá! —dijo Ven con mirada de pillín —Ya lo entiendo todo. Seguro que como  π servía para medir los círculos, el número de oro sirve para medir las estrellas de 5 puntas. ¡Soy un crack! 

Mati se rio y Sal miró a su hermano arrugando la nariz para subirse las gafotas.

—No, no exactamente. El número de oro, φ  es un número irracional como π, pero se encontró midiendo segmentos de rectas. Os lo explico con un dibujo, veréis.

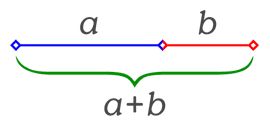
—En este dibujo, se cumple que 

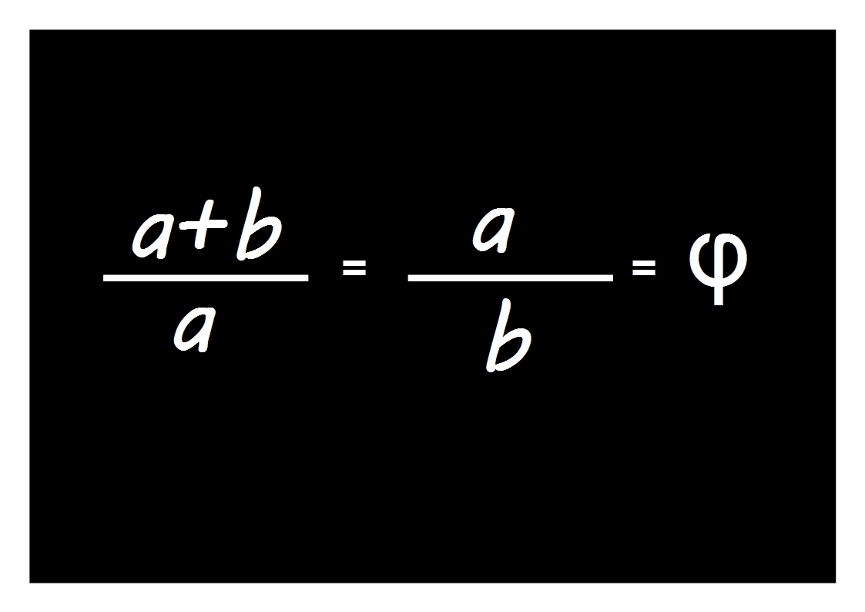
—Pero, ¿cuánto vale? —pregunta Ven que no entendía muy bien la sección aúrea.

Mati escribió en su pizarra

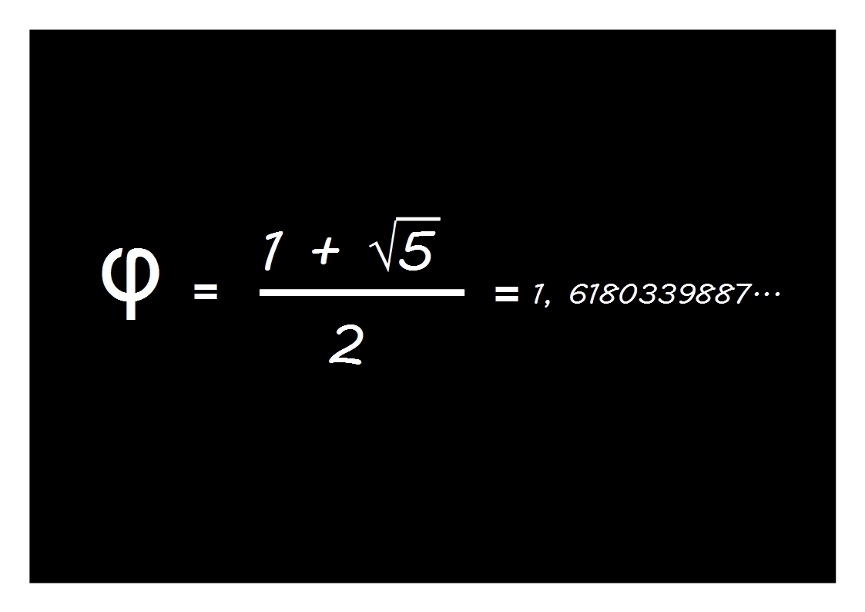
— Yo lo que no sé es qué tiene que ver φ con la estrella pitagórica… —masculló el gafotas.

—Ah, sí, es verdad. Os lo cuento ¿Qué queda si quitamos las 5 puntas?

—¡Un pentágono! —gritó Ven 

—Pues en ese pentágono, observad

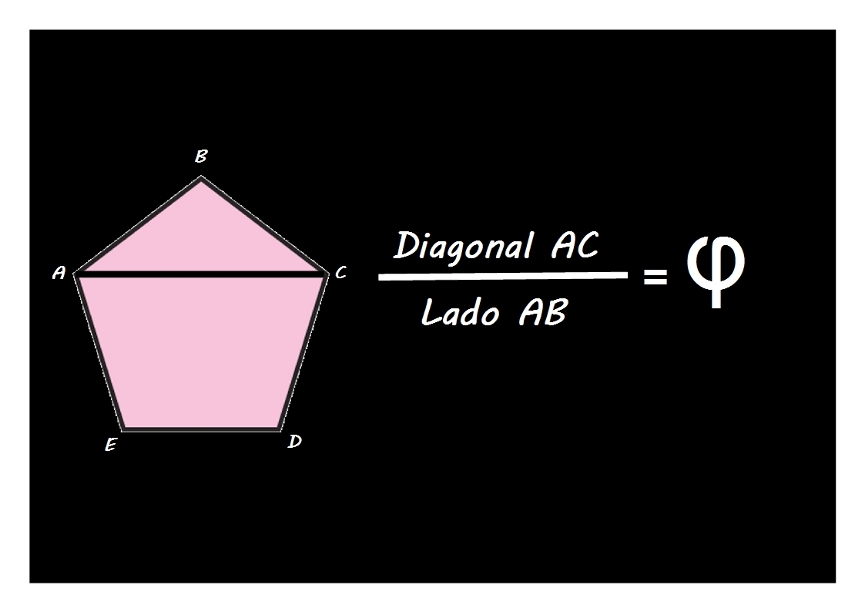
—Pero el número de oro está escondido en más sitios del pentagrama

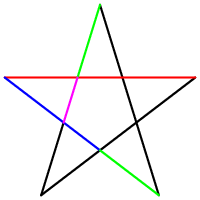
—Entonces —Mati escribió

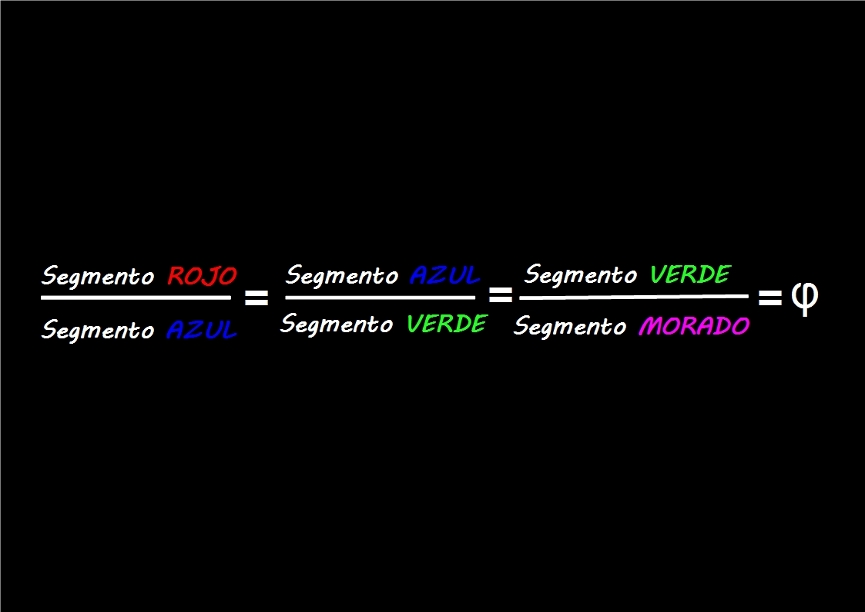
—¡Cómo mola Mati! —alucinaba Ven

—Y ese número de oro, ¿está sólo en el pentagrama? —preguntó Sal

—No, está en muchas figuras. Otra de la más conocidas es el rectángulo de oro, que es un rectángulo con la propiedad de que si divides el lado largo por el lado corto, te sale el número de oro. 

Por ejemplo, las tarjetas de crédito son rectángulos de oro. 

Se usa mucho, desde hace mucho tiempo en arquitectura, por ejemplo, está por todas partes en el Partenón de Atenas…

…en la catedral Notre Dame de París…

…en el cuadro de la Gioconda de Leonardo DaVinci…

—Mirad,  —siguió la gafotas —si queréis saber si un rectángulo es de oro, pedid una tarjeta de crédito prestada, y alejaos hasta que consigáis tapar el rectángulo con la tarjeta, alejándola con el brazo.
 

 

Pero no sólo en las matemáticas y en la arquitectura, sino que lo que más sorprende de este número de oro es que lo podemos encontrar en la Naturaleza: en el número de pétalos de las flores,en las espirales de una piña, el cociente entre vuestra altura y la altura de vuestro ombligo, o el de la distancia del hombro a los dedos y la distancia de los codos a los dedos. ¿Sabéis que es el ADN?

—No sé explicarlo muy bien —dijo Sal —pero es dónde está escrito de qué color son nuestros ojos y esas cosas, ¿no?

—Más o menos -contestó ella —Pues cada molécula de ADN es un rectángulo mágico, que mide 34 angstroms de largo por 21 angtroms de ancho.

—¿Un ans..qué? -preguntó Ven con la carita arrugada como una pasa

—Un angstrom, es una medida muy, muy pequeñita. Fíjate, Ven, en un centímetro que es esto —Mati separó las yemas de su pulgar y su índice aproximadamente un centímetro —hay 100 millones de angstroms.

—¡Toma, toma, toma! —el pequeño de la casa no daba crédito —Tiene que ser superdifícil escribir tan pequeñito…

—Bueno, Ven, no es exactamente así —le sonrió y le alborotó el cabello.

—¿Y por qué, Mati? ¿Por qué está en todas partes el número de oro? —interrumpió impaciente Sal.

—Porque las Matemáticas están en todas partes, cielo —sentenció la pelirroja con una sonrisa. Gauss ladró de contento, o eso creyeron nuestros amigos.

—Entonces, Mati, el pentagrama musical, ¿lo inventó Pitágoras con sus amigos? —quiso saber Sal

—No, para nada, el pentagrama musical, las 5 líneas paralelas que se usan hoy en día para escribir la música no se impuso hasta el siglo XVI. Antes de eso, desde el siglo X se usaron primero una línea roja que señalaba FA, luego añadieron una amarilla para DO, y después, un señor italiano llamado Guido D´Arezzo…

—¡Guido! ¡Como el amigo de Rayo McQueen! —gritó Ven asustando a Gauss.

— Sí, claro, pues eso, Guido D´Arezzo añadío 2 líneas mas, creando el tetragrama. En fin, que Pitágoras para esa época ya no estaba.

Sal esbozó una sonrisa pícara y Ven, apostilló, muy, muy serio:

—Pues vaya si es importante Patricio…

Bueno, no sé si Patricio es tan importante, el que sí que lo es, es el número φ. Hay infinidad de enlaces en la red para seguir averiguando cosas de este número ‘mágico’. Por ejemplo, éste en el blog de Alberto Piedrabuena; éste de Ignacio A. Langarita Felipe o éste de nuestros amigos de Sangakoo. Lo que sí os recomiendo es que si podéis, veáis la película Donald en el país de las Matemáticas, entre otras muchas cosas, explica muy bien el número de oro como veis en este vídeo:

Este otro vídeo también lo explica muy bien y con muchos ejemplos:

Y aquí podéis aprender a hacer estrellas con papel para hacer bonitos regalos 

Bueno, pues os dejo, me voy a buscar estrellas al mar. Hasta pronto