Con 3 esquinitas de nada...

—¡Pásamela, Elio!
—No puedo. Ven me la quiere quitar.
—Nunca podrás esquivar a Lionel Ven…¡soy un megaclack!

Mientras Sal, Ven y Elio (su primito) disputan en la arena de la playa su particular partido del siglo de esta semana, Gauss los observa con el ceño fruncido, como si de un entrenador jugándose la copa más grande y brillante de la historia del fútbol se tratase.

—¡Gol, gol, gol, gooooooooolazo! -grita Ven mientras corre lateralmente moviendo alternativamente sus manitas, arriba y abajo, con las yemas de los dedos de cada mano juntas.

Gauss se rasca con la pata, ¿tiene dudas?

—¡¡No es gol, Ven!! ¡¡Ha sido poste!! ¿Ves que has tirado la chancla de papá?

Y es que nuestros futbolistas usan las chanclas de sus padres para delimitar las porterías en la arena. Pero Ven seguía celebrando su tanto, ahora andando como Krabby, uno de sus Pokemon favoritos.

—Y además, mira dónde está el balón, lejísimo… —dijo Elio con voz preocupada.

Efectivamente, el balón, tras el potente lanzamiento de Ven Messi, había llegado a los pies de la torreta del vigilante de la playa, que no, no era el del coche fantástico. Cuando los tres primos llegaron junto a la pelota, el más pequeño de ellos, Elio, con los ojos como platos, exclamó:

—¡Wala! ¡Qué alto! Debe ser muy valiente para subir ahí.

—¡Bah! No es tan alto —contestó Ven—. La Giralda es más alta y yo he subido hasta arriba –remató con aire presumido.

—Hombre, claro, Ven, la Giralda mide 90 metros y esto… no sé, pero menos de 20 metros, seguro. -dijo el gafotas que por un momento había olvidado el falso gol de Ven y trataba de adivinar cuánto podía medir aquella torre.

—¿Le pedimos la cinta métrica al abuelo? -propuso Elio -Es muy larga, muy larga.

—Sí, claro, Elio —protestó Ven—, y ¿cómo subimos a medirla? ¿con un gorrocóptero? Ya te digo…

—No, pero podemos subir por las escaleras y dejar caer hacia abajo la cinta —dijo Elio.

—A mí me da yuyu subir —intervino Sal—. Además, estoy seguro de que nos iban a regañar…

Los tres estaban absortos mirando hacia arriba de la torre del vigilante.

—¿Qué buscáis, pequeños? —preguntó una voz conocida a sus espaldas.

—¡Hola Mati! —dijeron los tres a la vez.

Gauss se había acercado, le encantaba Mati y le gustaba escuchar lo que contaba.

—Mati, ¿cuánto crees que mide la torre del vigilante?

—Uy, yo soy malísima para ese tipo de estimaciones, pero si tenéis curiosidad lo podemos calcular.

—¿Tienes una cinta métrica? —preguntó Elio con una sonrisa de oreja a oreja.

—Sí, tengo cinta métrica.

—¿Y tienes gorrocópteros como Doraemon? —preguntó Ven—, ¿o tendremos que subir las escaleras?

—No, no tengo gorroc… ésos, eso no existe, sólo en nuestra fantasía, pero sí tengo Trigonometría.

—¿Trigo qué? —se extrañó Sal.

—Nuestra mamá no puede comer trigo —se apresuró a decir Ven, con cierto aire tristón—, sólo toma lasaña el día de mi cumpleaños, porque es mi comida favorita.

—Vaya… Pues sí, trigonometría es una palabra un poco rara, tenéis razón. Pero significa, más o menos, medir triángulos y se utiliza para muchas cosas.

—¡Para medir triángulos de las pizzas!

—Claro que sí, Elio, para los triángulos de las pizzas y para saber cuánto mide de alto esa torre del vigilante de la playa.

—Pero esta torre no es un triángulo, Mati…

—Ya lo sé, Sal, ¿queréis que os explique cómo se puede calcular la altura?

—¡Sí! —dijeron los 3 primos a la vez.

—A ver, a ver… Queridos ayudantes, necesito un palito pequeño o algo similar…

—Un momento —dijo Ven y salió corriendo hacía donde estaban su familia. Volvió enseguida con el bastón de clavar la sombrilla en la arena.

—¡Genial! —dijo la pelirroja—. Ahora lo clavaremos en la arena, muy derechito, para que forme un ángulo recto con el suelo.

—Ya estamos con los angulitos… —resopló Ven.

—Pero en este caso es muy fácil, Ven. Un ángulo recto es el que forman el larguero y el poste en una esquina de la portería:

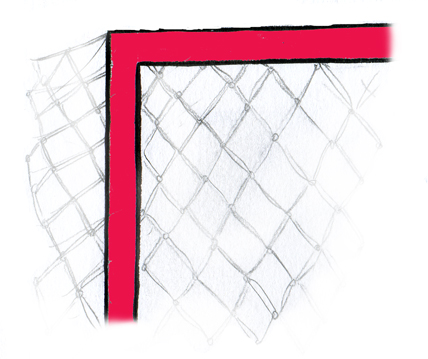
—Ah, vale —asintió sonriendo Ven a la explicación de Mati —¡como el córner!

—Ya está —dijo contento e ilusionado Elio que había ayudado a Sal a clavar el bastón en la arena, con mucha formalidad y profesionalidad.

—Vamos a medir la altura del bastón clavado en la arena.

Les dio una cinta métrica a los chicos que se pusieron con mucho interés a hacer su tarea.

—Un metro —dijo al fin Sal.

—Ahora, tenéis que medir la sombra del bastón.

—150 centímetros, Mati.

—Pues ya sólo nos falta medir la sombra de la torre -les indicó Mati.

Desarrollaron la cinta métrica pero sólo tenía 3 metros.

—No podremos medirla… —se lamentó Elio.

—Sí, basta con poner una marca en la arena y volver a medir, ¿no?

—¡Claro, Ven! —contestó Sal mirando a su hermano pequeño con admiración y sintiéndose él mismo orgulloso de todo lo que había enseñado ya.

Pues la sombra medía tanto como 5 cintas métricas.

—5×3=15 —concluyó Ven.

—15 metros, Mati —dijo Elio.

—Como hemos medido las sombras a la misma hora, podemos considerar que los rayos del sol sobre el bastón y la torre forman el mismo ángulo.

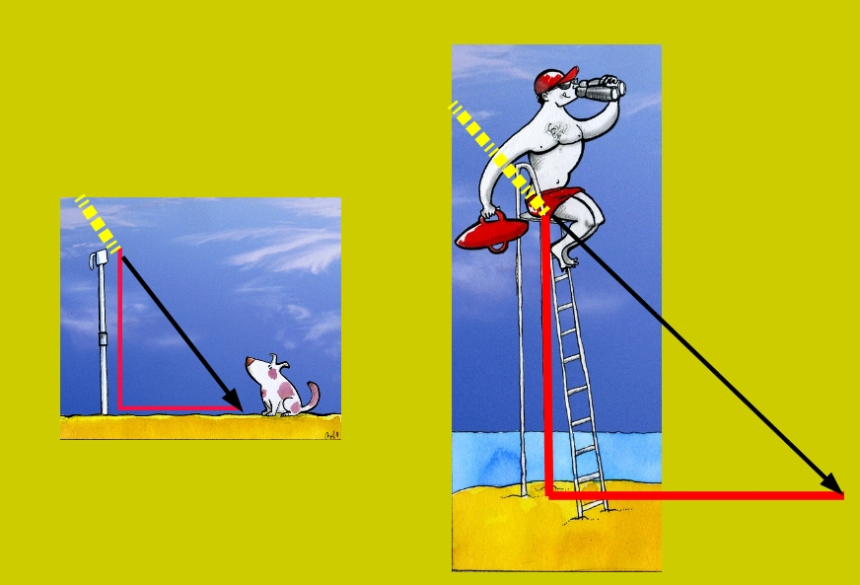
—Esto significa que estos dos triángulos son semejantes, porque tienen iguales todos los ángulos.

—Uno no lo sabemos, el de la sombra con el rayo… —dijo con un poco de recelo Sal

—Y no hace falta, porque los ángulos de un triángulo siempre suman lo mismo, 180º. Los dos tienen un ángulo recto con el suelo, el del sol es igual, por lo tanto el otro también debe ser el mismo.

—Entonces, por ser semejantes tenemos:

y por eso

—¡Wow! ¡Cómo mola, cómo mola! —decía Ven llevándose la mano derecha a la frente en señal de asombro absoluto.

Elio seguía con la boca abierta y Sal seguía con el ceño fruncido pensando algo, hasta que finalmente preguntó a su amiga:

—Entonces, si sabes cuánto mide de alto también podrías calcular hasta dónde llegaría la sombra de la torre, ¿no?

—Claro que sí, mira:

—¡Qué chulo es todo esto, Mati! Me encanta.

—Ya te dije que los triángulos eran muy “apañaos”, a mí me encantan.

—Y con 3 esquinitas de nada… —seguía asombrado nuestro gafotas.

—¿Podemos dejar un poco los triángulos y seguir con el partido? —preguntó Ven que se sentía engrandecido con el tanto obtenido antes de toda esta trigonometría.

—Claro que sí, cielo —dijo Mati—, pero que sepas que en el fútbol también se usan los triángulos.

—No estoy seguro —contestó Ven con los labios en horizontal.

—¿Los jugadores no triangulan?

—¡Toma! ¡Es verdad!

—Además, si quieres, te enseño un truco para encontrar el mejor punto para lanzar a la portería desde la banda.

—¿En serio?

—Claro, mira a estas posiciones, 1, 2 y 3, en la banda y dime cuál es la mejor para lanzar a la portería.

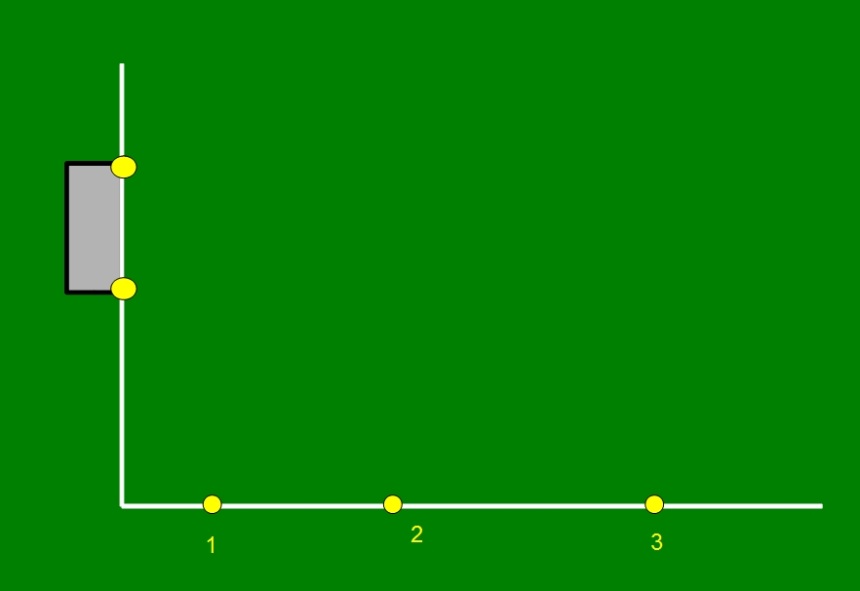
Después de mirar con detenimiento los gráficos, Ven eligió la 1.

—¿Por qué ésa, cielo?

—Porque está más cerca.

—Pero tiene menos ángulo para disparar entre los palos, mira:

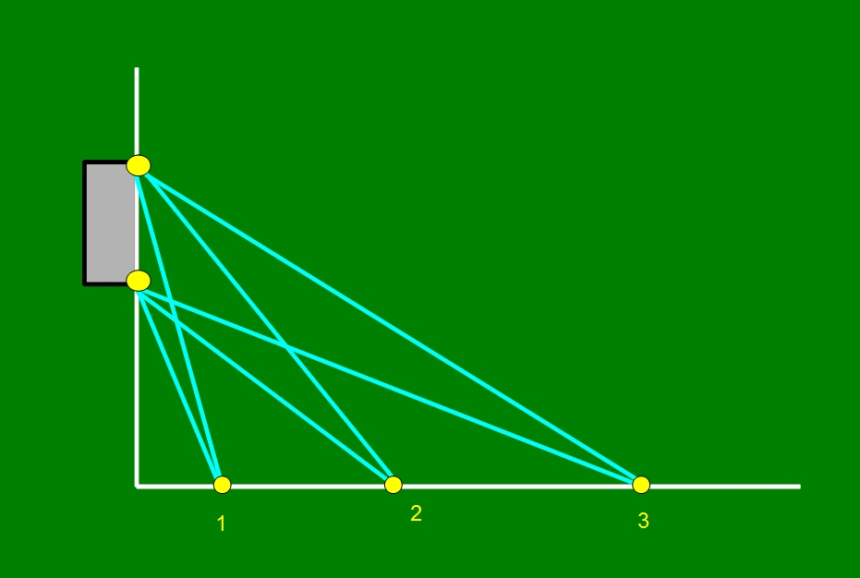
—Ah, entonces… la 2 —dijo Ven victorioso.

—Efectivamente, para conseguir mayor amplitud de ángulo de lanzamiento, tienes que ponerte de tal forma que el círculo que pasa por tu posición y los dos postes sea tangente a la banda, sólo toque en un punto, el de tu posición. Es decir, de todos los posibles círculos que pasan por los dos postes, elegir el único que toque a la banda en un sólo punto y colocarte ahí. Fíjate en el siguiente dibujo:

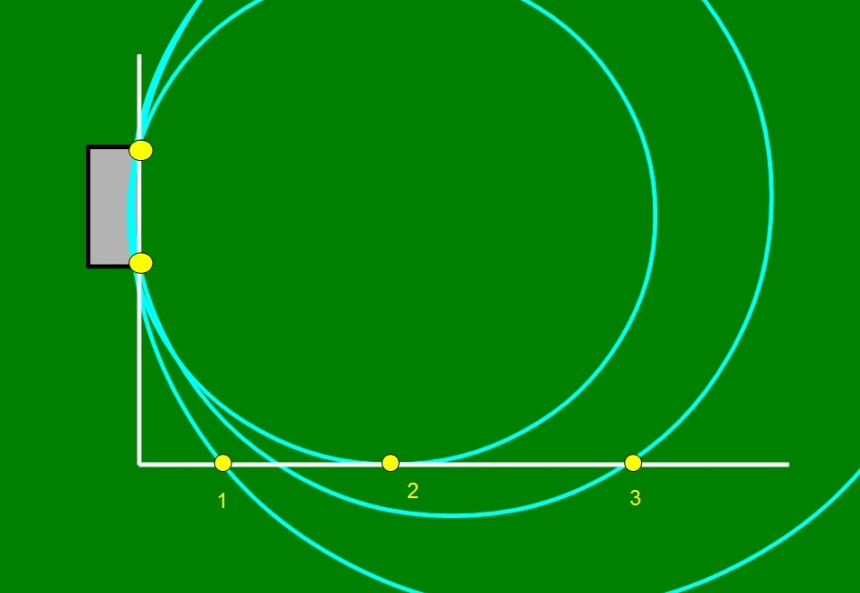
Ven se quedó muy serio pensando durante unos minutos, con la mirada perdida hacia arriba y hacia la izquierda…

—Mati, no creo que los futbolistas lo hagan así, ¿eh? -dijo prudentemente para no molestar a su amiga.

—Puede que no, cielo, pero deberían —le contestó ella con una sonrisa y un guiño.

—Ven, vamos a jugar ya, ¿no? —suplicó Elio.

Los 3 niños salieron corriendo mientras ella los miraba desde lejos sonriendo. En ese momento bajó el vigilante, llegaba su relevo, e invitó a Mati a una limonada a cambio de que le explicara lo que le estaba explicando a los niños.

—¡¡¿¿Pero qué estás haciendo Ven??!! ¡¡Saca ya!! —gritó Sal impaciente.

—Espera, espeeeeeeera… que tengo que dibujar mentalmente un círculo…

Pues efectivamente, la trigonometría y los triángulos tienen un montón de aplicaciones, ésta es sólo una de ellas, pero os iré contando muchas más, poco a poco.

Lo de medir la torre usando el bastón de la sombrilla no lo he descubierto yo, ¿eh?. Cuenta una leyenda (relatada por Plutarco) que Thales de Mileto (un señor muy listo de la antigua Grecia, aunque actualmente Mileto está en territorio de Turquía) en un viaje a Egipto, visitó las pirámides y admirado ante tan grandiosos monumentos quiso saber su altura. Y lo hizo como lo hemos hecho nosotros, estableciendo así el primer Teorema de Thales.

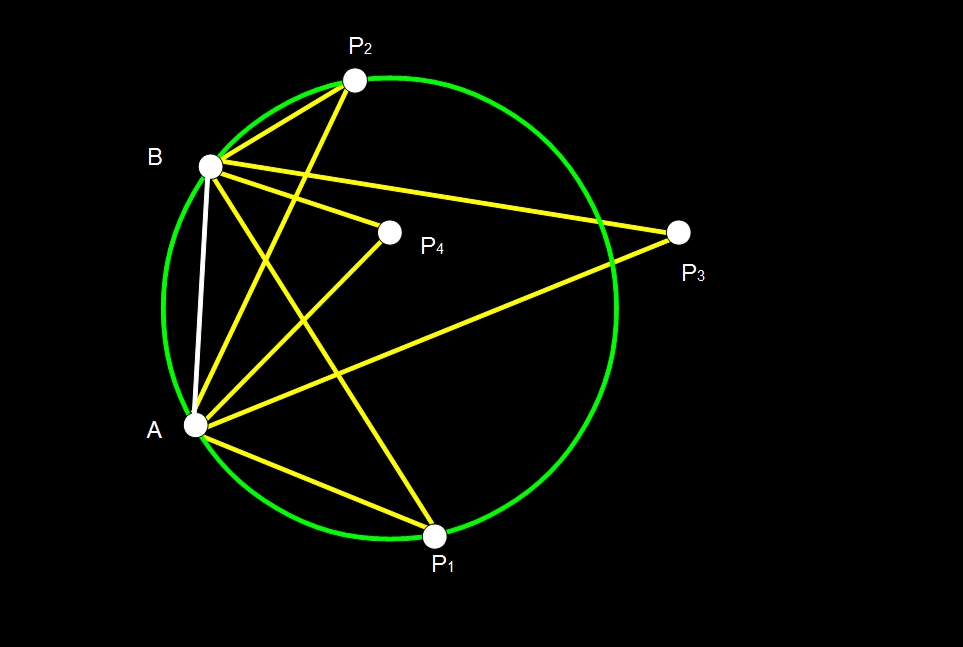
En cuanto el “truco” del saque de banda… se trata solamente de una consecuencia del Segundo Teorema de Thales que nos permite asegurar que dada una circunferencia (que llamaremos C) y una cuerda (segmento uniendo dos puntos cualesquiera de la misma), en la figura AB, en cualquiera de los dos semiplanos que define la recta que contiene a esa cuerda, los puntos interiores a C (por ejemplo P₄ ) ‘ven’ a AB con mayor ángulo que cualquier punto sobre C (por ejemplo P₁ y P₂), y a su vez, cualquier punto sobre C la ve con mayor ángulo que cualquier punto exterior, por ejemplo P₃.

Es más, todos los puntos sobre C, como P₁ y P₂, ven la cuerda AB con el mismo ángulo y dicho ángulo es recto si y solamente si, la cuerda AB coincide con un diámetro, esto es, si la cuerda AB pasa por el centro de C.

Y si no lo habéis entendido, os dejo este vídeo que os lo explica muy bien.

Hasta pronto.

El título de esta entrega de Mati está inspirado en el título del cuento de Jèrôme Ruillier, Por cuatro esquinitas de nada, uno de los cuentos favoritos de mis hijos y también mío (a pesar de que no salgan triángulos), una maravillosa, elegante y ‘geométrica’ llamada a la tolerancia con los que son diferentes a nosotros.